Find the area of the flower bed (with semi-circular ends) shown in figure.

Video Solution
Text Solution
Length and breadth of a circular bed are 38 cm and 10 cm .
∴ Area of rectangle ACDF = Length×Breadth=38×10=380cm2
Both ends of flower bed are semi-circles.
∴ Redius of semi-circle= DF2=102=5cm
∴ Area of one semi-circles = πr22=π2(5)2=25π2cm2
∴ Area of two semi-circles= 2×252π=25πcm2
∴ Total area of flower bed = Area of rectangle ACDF + Area of two semi-circles
= (380+25π)cm2

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the area of the shaded region. [All the circles shown in the figure are congruent]
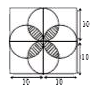 A22(π2−1)B50πC100(π2−1)D200(π−1)
A22(π2−1)B50πC100(π2−1)D200(π−1)An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200m as shown below:
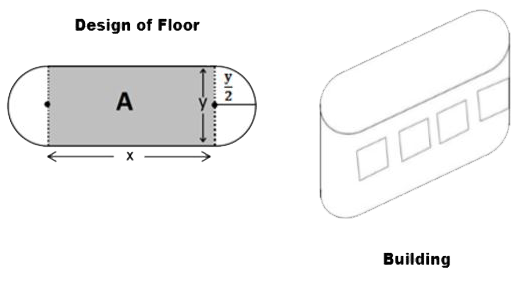
based on the above information answer the following
The CEO of the multi-national company is interested in maximizing the area of the whole floor including the semi-circular ends. For this to happen the valve of x should beA0mB30 mC50 mD80m
Find the magnetic field at the centre of the circular loop shown in figure.

View SolutionFind the magnetic field at the centre of the circular loop shown in figure.

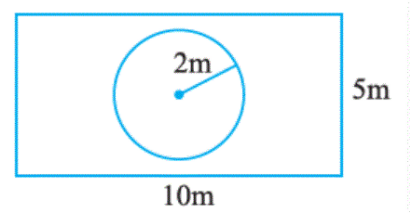
View SolutionThe adjoining figure represents a rectangular lawn with a circular flower bed in the middle. Find:
(i) the area of the whole land
(ii) the area of the flower bed
(iii) the area of the lawn excluding the area of the flower bed
(iv) the circumference of the flower bed.
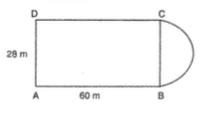
View SolutionA plot is in the form of a rectangle ABCD having semi-circle on BC as shown in Figure. If AB=60m and BC=28cm, find the area of the plot.
View SolutionFind the area of the shaded field shown in figure.

View SolutionFind the area of the shaded field shown in figure.
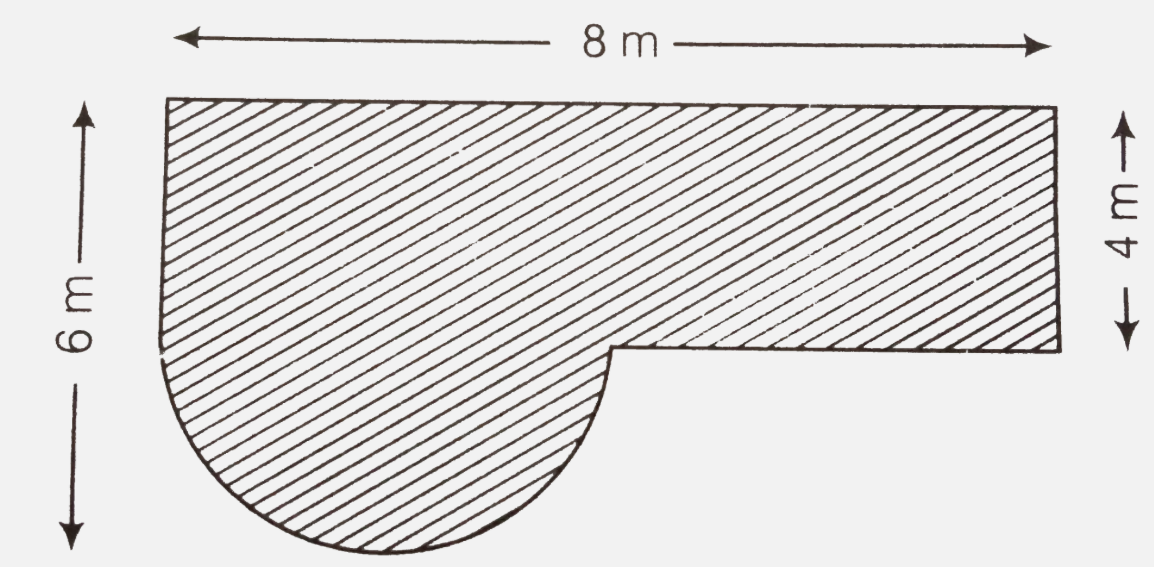
View Solution


