In the given figure ABCD is a trapezium in which and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm hav been drawn with centres A,B,C and D then find the area of the shaded region.

Given, AB = 18cm, DC = 32 cm, height, (h) = 14cm
and arc of radii = 7 cm
Since, AB || DC
and
Area of sector with angle A and
=
=
similarly, area of sector with angle B and C = 77cm
Now, area of trapezium =
=
Area of shaded region = Area of trapezium - (Area of sector points A and D + Area of sector points B and C)
=
Hence, the required area of shaded region is .
Topper's Solved these Questions
Similar Questions
Combination of quadrilateral and circle : In Figure; ABCD is a trapezium with AB||DC ; AB = 18cm; DC = 32cm and the distance between AB and DC is 14 cm. Circles of Equal radii 7 cm with centres A;B;C and D have been drawn. Then; find the area of the shaded region of the figure.
View SolutionIn the given figure ABCD is a trapezium in which AB∣∣DC and AB:DC=3:2, The ratio of the areas of △AOB and △COD is
View Solution
Knowledge Check
In figure, ABCD is a trapezium in which AB I I DC. Find the length of DC.
 A17 cmB11 cmC13 cmD15 cm
A17 cmB11 cmC13 cmD15 cm
In the following figure ABCD is a trapezium in which AB∣∣DC. Find the measdure of ∠C.

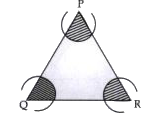
View SolutionIn figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .

View SolutionIn the given figure, ABCD is a trapezium in which AB = 9 cm, AD = BC= 6 cm, DC = x cm, and distance between AB and DC is 2√5 cm. The value of area of trapezium ABCD is k√5. Find the value of k.

View SolutionIn the given figure, arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionABCD is a trapezium in which AB || DC, ABデ78 cm, CD = 52 cm. AD = 28 cm and BC =30cm . Find the area of the trapezium.
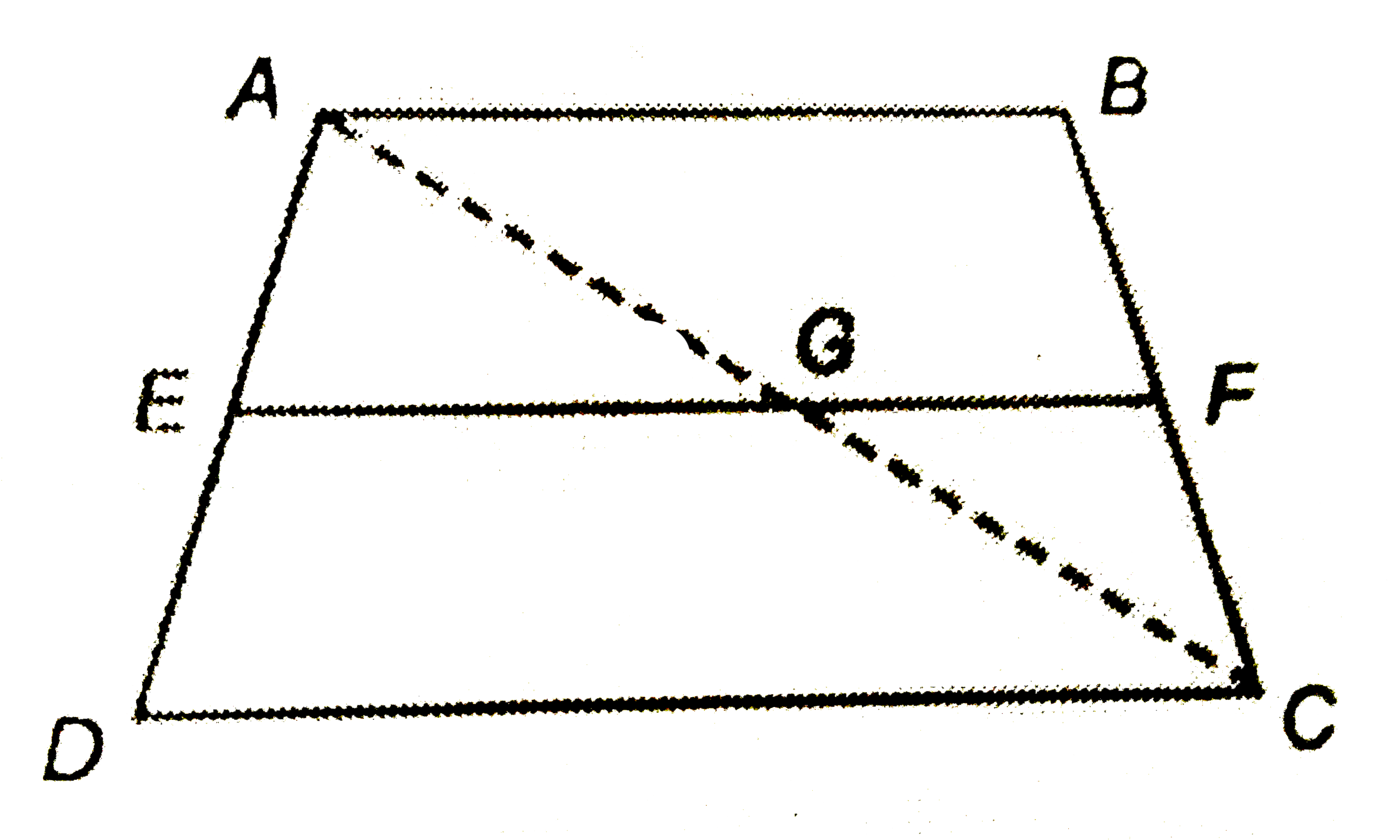
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
View Solution
