A uniform magnetic field is applied in a circular region of radius R as shown in the given figure. A charged particle of charge q and mass m enters with a velocity from point P along the line that is making an angle with the line segment OP, in the region of magnetic field.
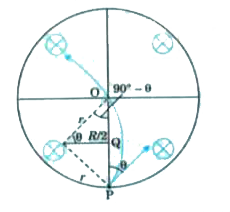
The charged particle is found to pass through the centre of the circular region. Find the angle θ.
Given : B=1T,R=10cm,m=6×10−3kg,q=6×10−2C,v=1/√3.
from the figure it can be easily understood that the locus of the charged particle is symmetric about point Q .
Radius of the path followed by the particle can be written as follows:
r=mvqB=6×10−3×1/√36×10−2×1=110√3m
Refer the figure again to understand the following:
cosθ=R/2r=(0.1)210√3=√32
Here , θ=30∘.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Textbook Exercises)
13 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - NCERT FILE (NCERT Additional Exercises)
15 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Conceptual Questions
29 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
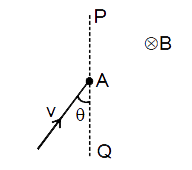
impulse of magnetic force.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
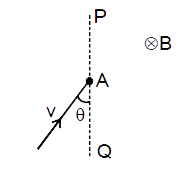
distance travelled in the magnetic field
View Solution
Knowledge Check
A charged particle of charge Q and massm moves with velocity v in a circular path due to transverse magnetic field, B, then its frequency is
AQB2πmBQvB2πmCQmvB2πDvb2πQmA charged particle enters into a magnetic field with velocity vector making an angle of 30∘ with respect of the direction of magnetic field. The path of the particle is
AcircularBhelicalCellipticalDstraight lineA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of B
A positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
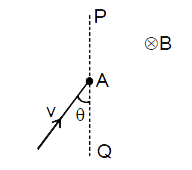
time spent
View SolutionA uniform magnetic field of intensity 1T is applied in a circular region of radius 0.1m, directed into the plane of paper. A charged particle of mass 5×10−5kg and charge q=5×10−4C enters the field with velocity 1/√3m/s making an angle of ϕ with a radial line of circular region in such a way that it passes through centre of applied field the angle ϕ is
View SolutionA charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
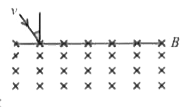
View SolutionA charged particle having charge 2q and mass m is projected from origin in X-Y plane with a velocity v inclined at an angle of 45∘ with positive X-axis in a region where a uniform magnetic field B unit exists along +z axis. The coordinates of the centre of the circular path of the particle are
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View Solution
