Question

The path of a charged particle moving in a uniform steady magnetic field cannot be a

Explanation

Let us visualise a uniform magnetic field within a given width as shown in the figure.

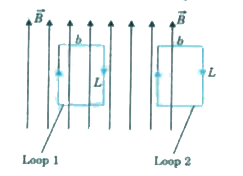
We have shown two Amperian loops in rectangular form with dimensions, `L xx b.` Loop 1 is completely inside the magnetic field and loop 2 is at the boundary where magnetic field is shown to end abruptly.
First of all let us look at loop 1. Two sides of this loop are perpendicular to the magnetic field and hence `vecB * d vecl = 0 ` for these two sides. Let the sense of the loop assumed be as shown in the figure so `vecB * d vecl` for the remaining one arm is BL and for the other it is` -BL` and these two add up to zero. Hence total circulation of magnetic field is zero for loop A.
According to Ampere.s law, the circulation of magnetic field must be equal to Ho multiplied with enclosed current. Hence, the enclosed current in loop A must be zero. From this condition we can conclude that there will not be any current inside the uniform magnetic field.
Now let us look at loop 2. One side of loop 2 is outside the field and similar to loop A, if we calculate then we will get the net circulation for loop B equal to BL, because one side is outside the field and there is no cancellation like in loop 1. It is non-zero. Again, according to Ampere.s law there must be some enclosed current within this Amperian loop B due to non-zero circulation of magnetic field. But we have already proved that no current will be enclosed within the uniform field. Hence, there is discrepancy near the boundary. The fact is that a uniform magnetic field can never end abruptly like this in real life.