A long wire carrying a current i is bent to form a plane angle θ. The magnetic field at a point on the bisector of this angle situated at a distance d forms vertex is
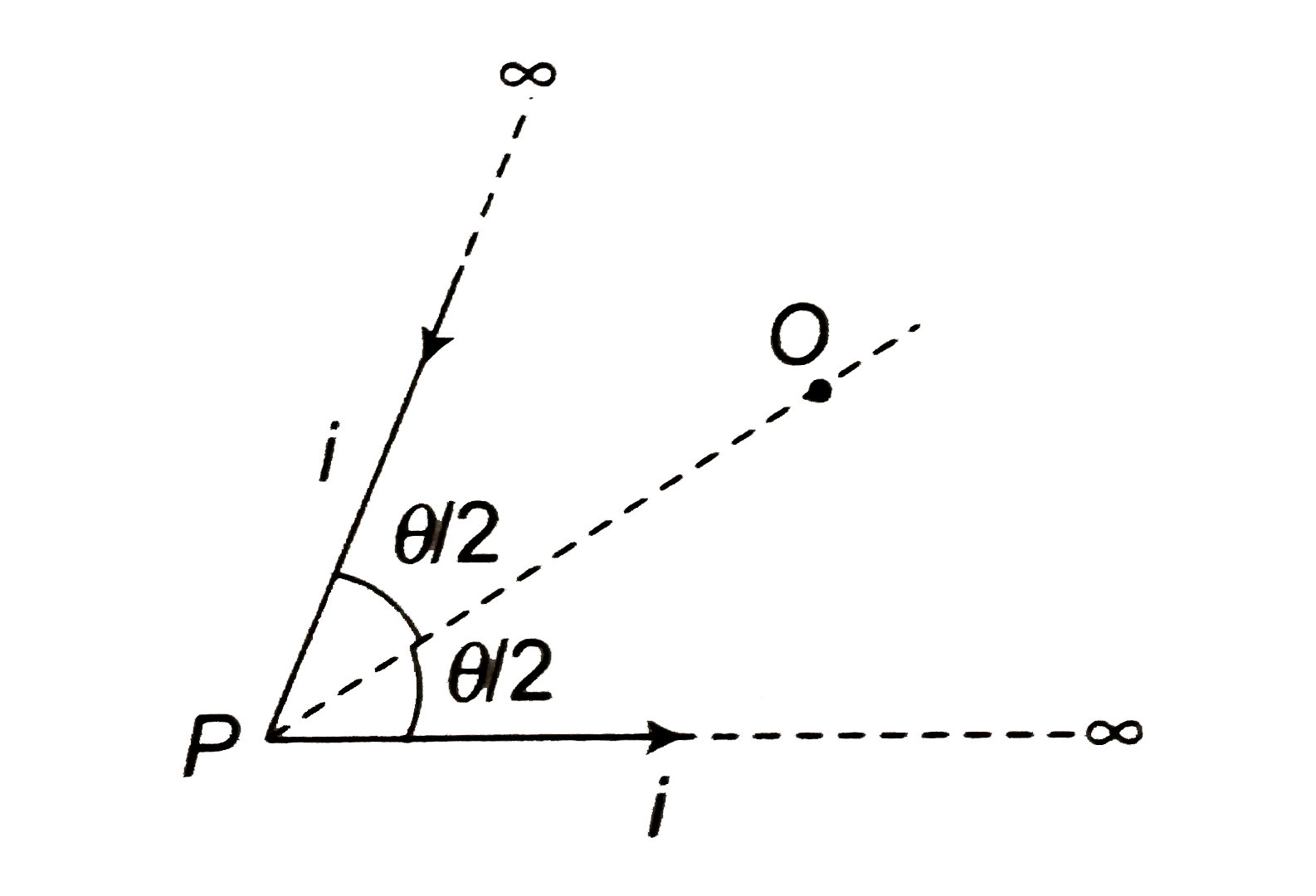
Two straight parts of the system will create the same magnetic field in the same direction and hence we can multiply the result for one half of the system by two.

Magnetic field intensity due to a straight wire of finite length can be written as follows:
B=μ0I4πd(sinα+sinβ) ....(i)
In the given situation as per figure α=90∘−θ and β=90∘ due to infinite length on one side.
Here, the value of d can be calculated from triangle OPQ.
sinθ=dx⇒d=xsinθ
We can substitute these values in equation (i) and multiply the result with 2 to compensate for the second half of the system. Hence, the net magnetic field intensity can be written as follows:
B=2×μ0I4πxsinθ[sin(90∘−θ)+sin90∘]
⇒ B=μ0I2πxsinθ[cosθ+1]=μ0I2πx(1+cosθsinθ)
⇒ B=μ0I2πx2cos2.θ22sin.θ2cos.θ2=μ0I2πxcos.θ2
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT FILE (NCERT Textbook Exercises)
Explore 13 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT FILE (NCERT Additional Exercises)
Explore 15 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Conceptual Questions
Explore 29 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
Find magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)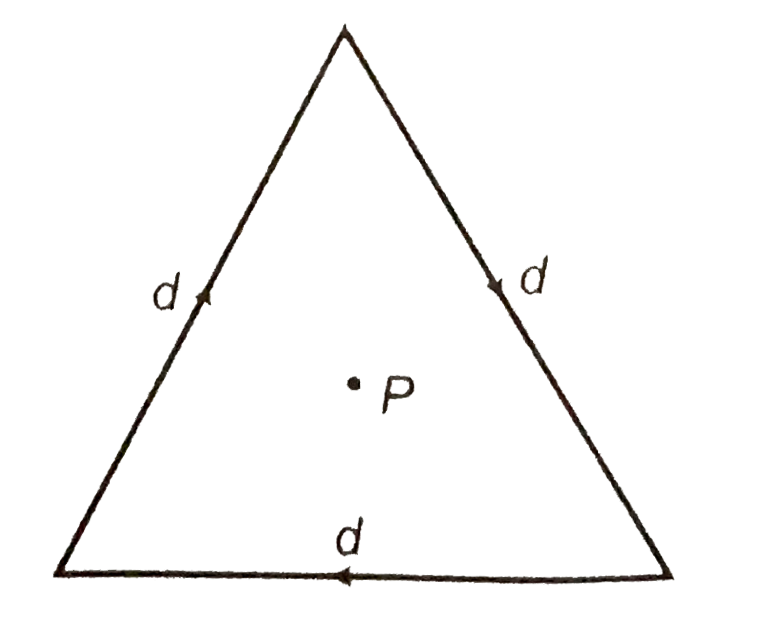
P is the centre of equilateral triangle.
(d)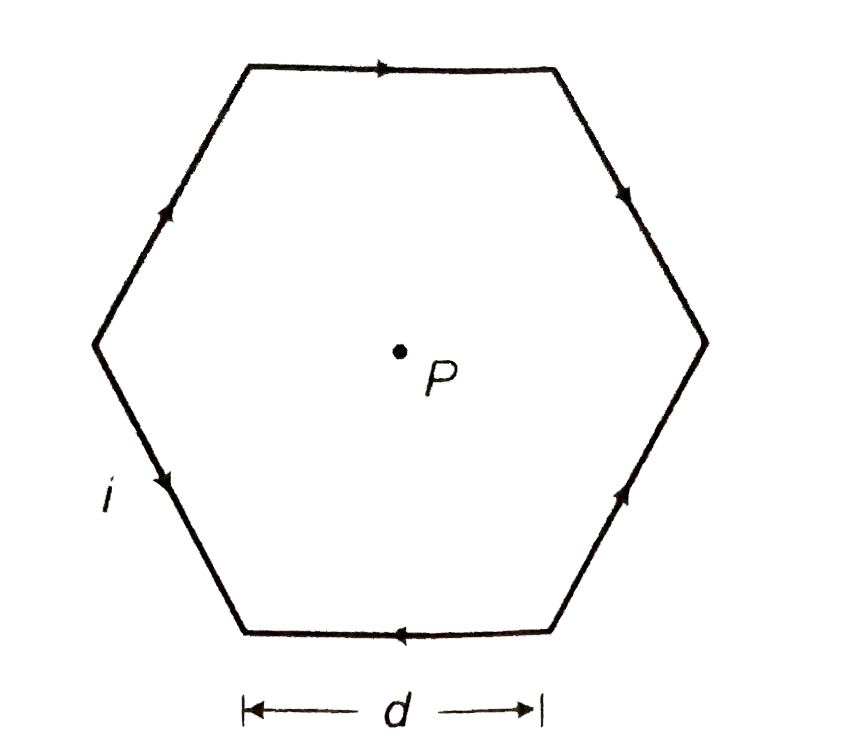
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)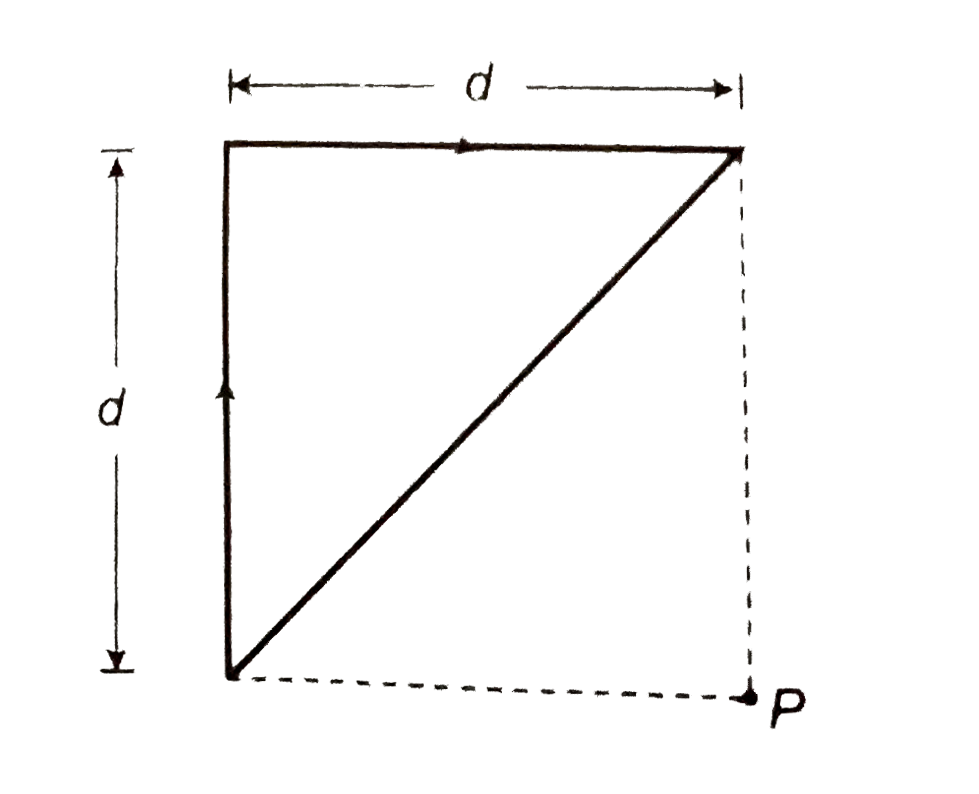
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionAlongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View Solution
Knowledge Check
A long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
A√2μ0i4πdB3√2μ0i4πdC5√2μ0i4πdD7√2μ0i4πdA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)
 A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πd
A2μ0I2πdBμ0I2πdCμ0I√3πdD√3μ0I2πdA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
A long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
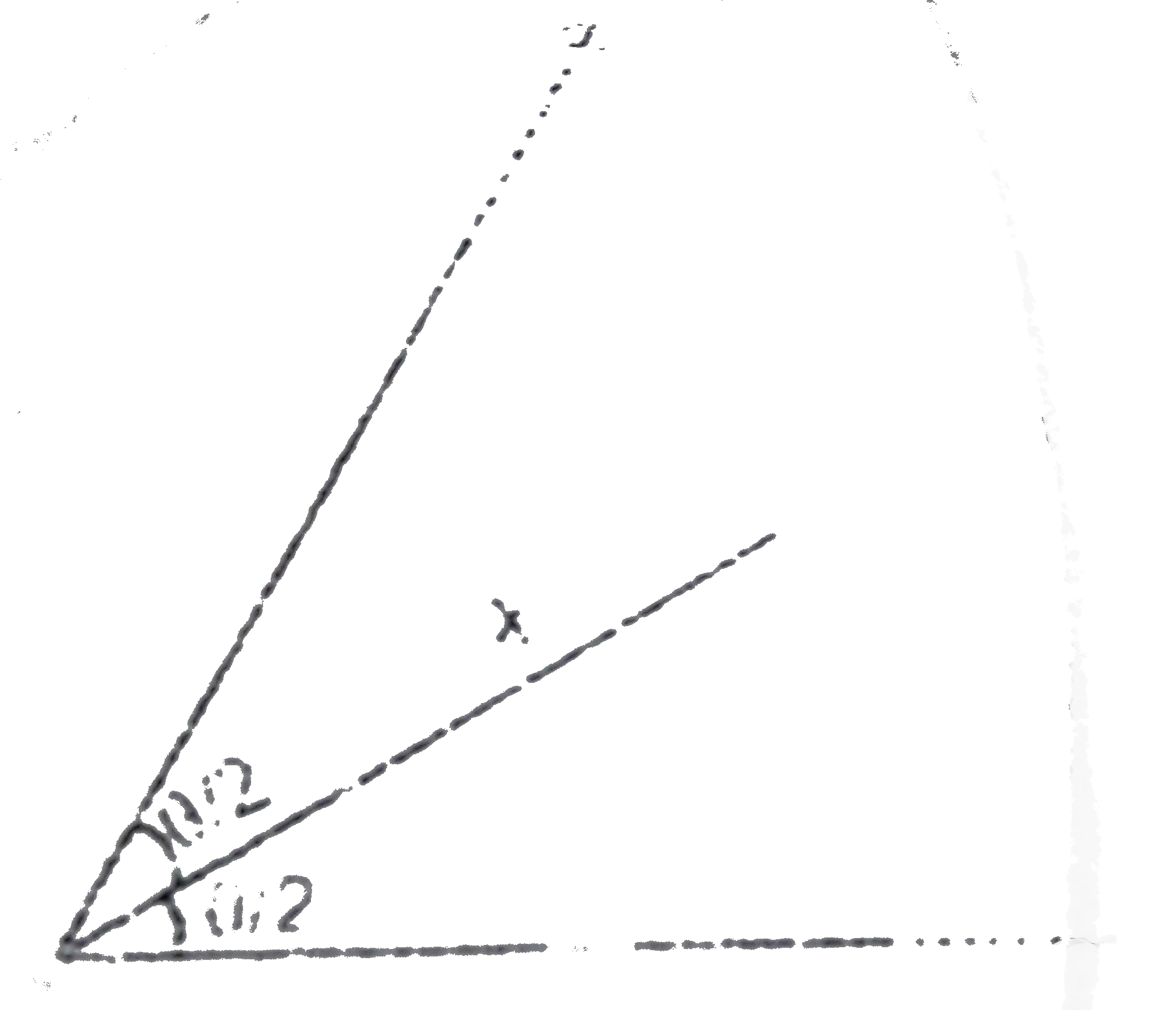
View Solution(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
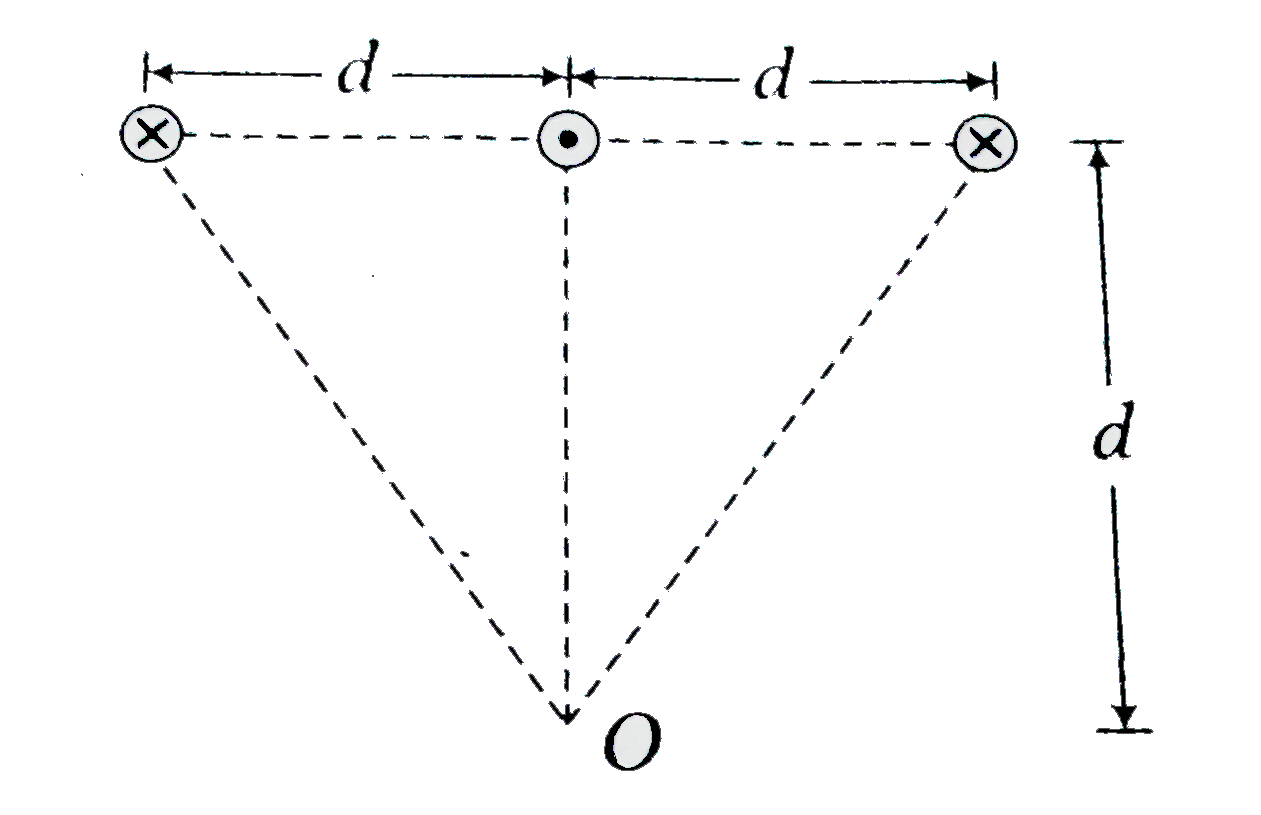
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View SolutionA wire of length 2 m carrying a current of 1 A is bent to form a circle, the magnetic moment of the coil is
View Solution

