A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section. Let B2 be the magnetic field at this point due to this section only. Find the value of d/l so that B2 differs from B1 by 1 %.
We know that the magnetic field due to an infinitely long wire is given by the following relation:
B1=μ0i2πd …(i)
Now let us find that magnetic field due to l length on its perpendicular bisector. Here for perpendicular bisector,
sinα=sinβ=l/2√d2+l2/4=l√l2+4d2
Magnetic field can be written as follows:
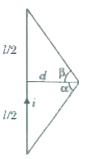
B2=μ0i4πd(sinα+sinβ)
⇒ B2=μ0i4πd(2×l√l2+4d2)
⇒ B2=μ0i2πd(l√l2+4d2) ....(ii)
Difference between B1 and B2 is 2% .
⇒ B1−B2B1×100=2
⇒ 1−B2B1=150
Substituting the values in equations (i) and (ii) we get the following:
⇒ 1−l√l2+4d2=150
⇒ 1−(1+4d2l2)−1/2=150
⇒ 1−(1−2d2l2)≈150
⇒ d2l2=1100
⇒ dl=110
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT FILE (NCERT Textbook Exercises)
Explore 13 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:NCERT FILE (NCERT Additional Exercises)
Explore 15 Videos
- MOVING CHARGES AND MAGNETISMBook:MODERN PUBLICATIONChapter:MOVING CHARGES AND MAGNETISMExercise:Conceptual Questions
Explore 29 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
Similar Questions
Find magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)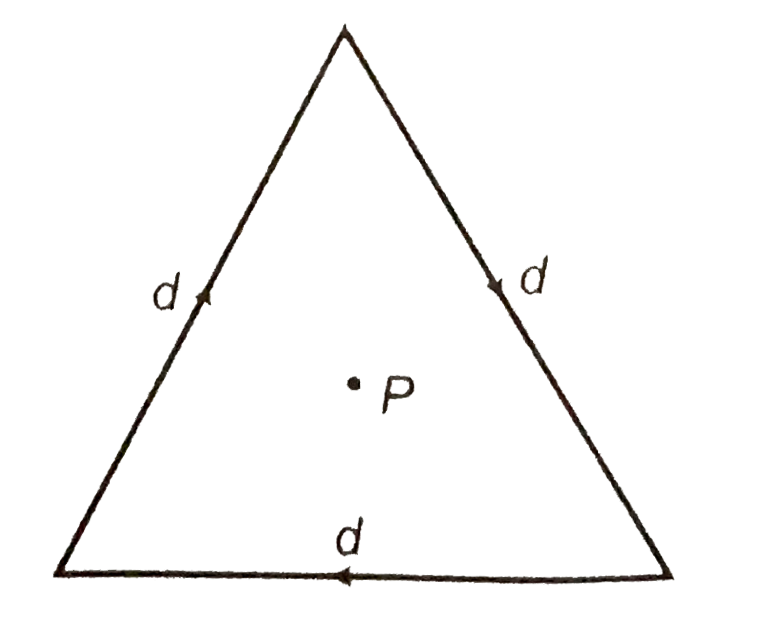
P is the centre of equilateral triangle.
(d)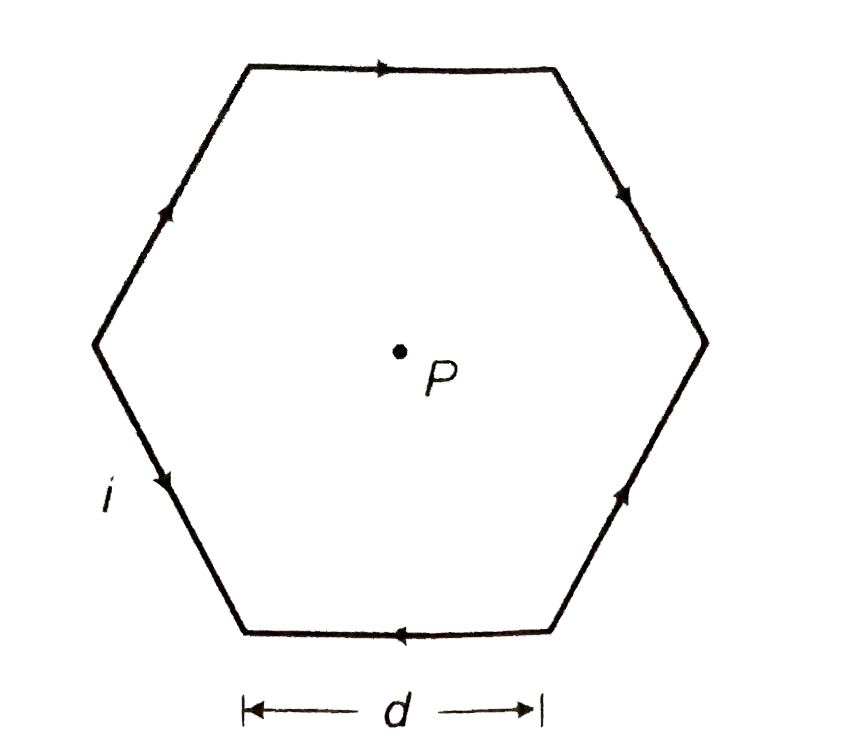
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)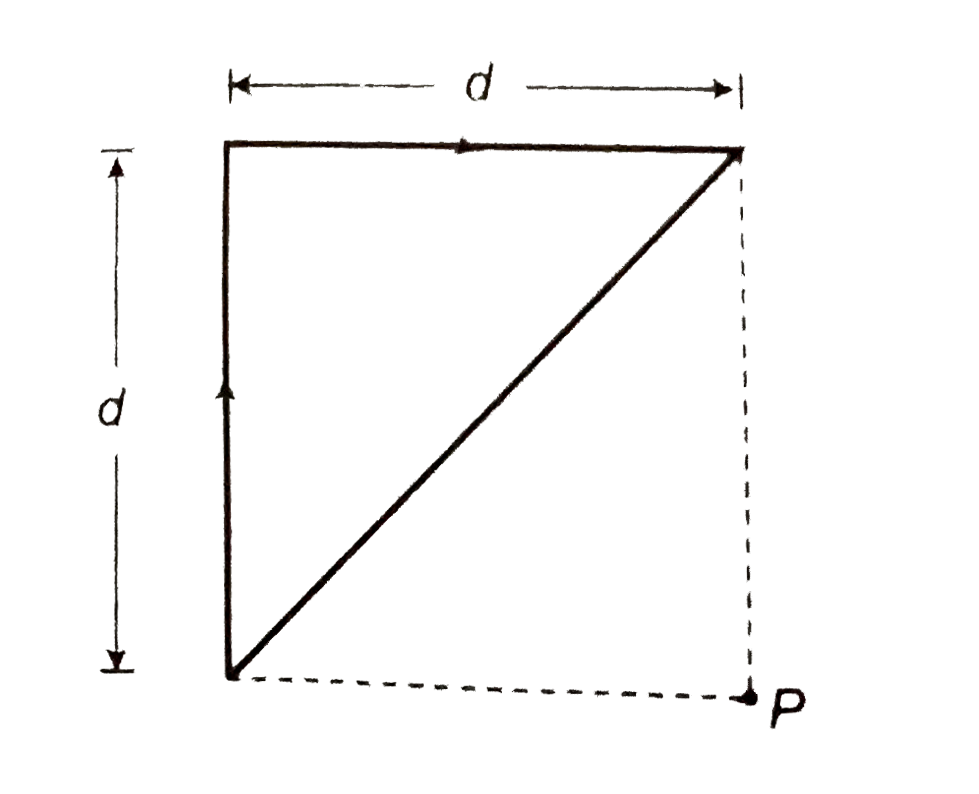
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionA long straight wire carries a current of 35A. What is the magnetic of the field →B at a point 20cm from the wire?
View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5TA long, straight wire carries a current i. The magnetizing field intensity H is measured at a point P close to the wire. A long, cylindrical iron rod is brought close to the wire so that the point P is at the centre of the rod. The value of H at P will
Aincrease many timesBdecrease many timesCremain almost constantDbecome zero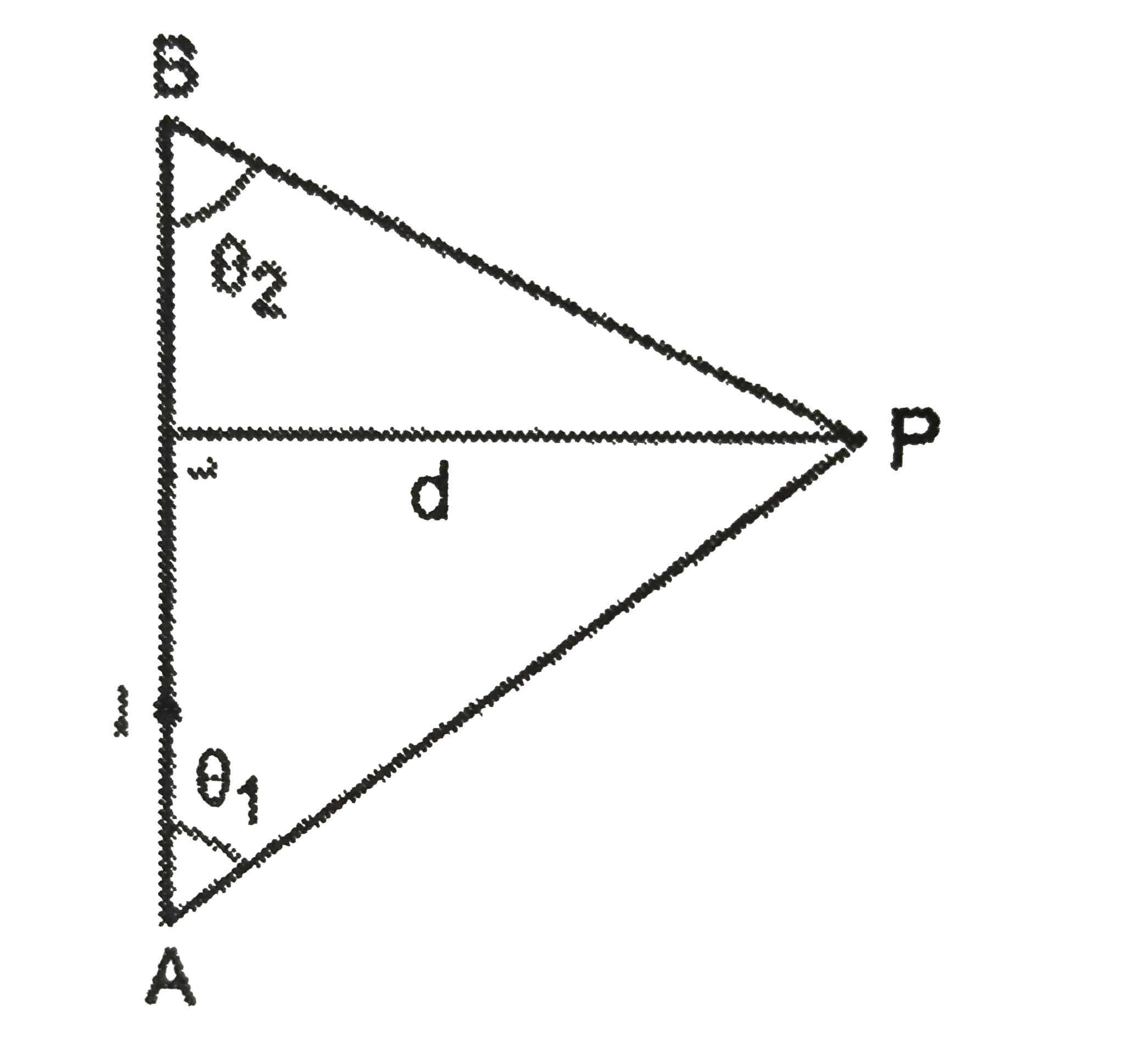
AbB is a section of a straight wire carrying a current I. P is a point at a distance d from AB. The magnetic field at P due to AB has magnitudeAμ0I4πd(cosθ1+cosθ2)Bμ0I4πd(cosθ1−cosθ2)Cμ0I4πd(sinθ1+sinθ2)Dμ0I4πd(sinθ1−sinθ2)
Calculate the magnetic field induction at a point distance, a√32 metre from a straight wire of length 'a' metre carrying a current of i amp. The point is on the perpendicular bisector of the wire.
View SolutionA wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?

View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View SolutionA very long straight wire of radius 'r carries current 'I'. Intensity of magnetic field 'B' at a point, lying at a perpendicular distance 'a' from the axis is ∝ ___________
View Solution

