Calculate the magnetic field induction at a point distance, a√32 metre from a straight wire of length 'a' metre carrying a current of i amp. The point is on the perpendicular bisector of the wire.
To calculate the magnetic field induction at a point distance (a√32) metres from a straight wire of length a metres carrying a current i amperes, where the point is on the perpendicular bisector of the wire, we can follow these steps:
Step 1: Understand the Geometry
We have a straight wire of length a carrying a current i. The point where we need to calculate the magnetic field is located on the perpendicular bisector of the wire at a distance of a√32 from the wire.
Step 2: Identify the Relevant Angles
Since the point is on the perpendicular bisector, we can determine the angles formed between the wire and the line connecting the wire to the point. The distance from the midpoint of the wire to the point is a√32, and the half-length of the wire is a2.
Using trigonometry, we can find the angle θ at which the magnetic field contributions from each segment of the wire will be calculated.
Using the tangent function:
tan(θ)=oppositeadjacent=a2a√32=1√3
This implies that θ=30∘.
Step 3: Calculate the Magnetic Field
The formula for the magnetic field B at a distance d from a long straight wire carrying current i is given by:
B=μ0i4πd⋅(sinθ1+sinθ2)
Where:
- d is the perpendicular distance from the wire to the point,
- θ1 and θ2 are the angles corresponding to the two ends of the wire.
Since both angles are 30∘:
sin(30∘)=12
Thus,
B=μ0i4π(a√32)⋅(12+12)
B=μ0i4π(a√32)⋅1
B=μ0i2πa√3
Step 4: Final Result
The magnetic field induction at the point is:
B=μ0i2πa√3 Tesla
We have a straight wire of length a carrying a current i. The point where we need to calculate the magnetic field is located on the perpendicular bisector of the wire at a distance of a√32 from the wire.
Since the point is on the perpendicular bisector, we can determine the angles formed between the wire and the line connecting the wire to the point. The distance from the midpoint of the wire to the point is a√32, and the half-length of the wire is a2.
tan(θ)=oppositeadjacent=a2a√32=1√3
This implies that θ=30∘.
The formula for the magnetic field B at a distance d from a long straight wire carrying current i is given by:
B=μ0i4πd⋅(sinθ1+sinθ2)
Where:
- d is the perpendicular distance from the wire to the point,
- θ1 and θ2 are the angles corresponding to the two ends of the wire.
sin(30∘)=12
Thus,
B=μ0i4π(a√32)⋅(12+12)
B=μ0i4π(a√32)⋅1
B=μ0i2πa√3
The magnetic field induction at the point is:
B=μ0i2πa√3 Tesla
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-1
50 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
Knowledge Check
A wire of length L metre carrying a current of I ampere is bent in the form of a circle. Find its magnetic moment.
A1πL2/4Am2B21L2/πAm2C1L2/4πAm2D1L2/4Am2What is the magnetic induction at a distance of 5 cm from a straight wire carrying a current of 5 mA ?
A4×10−8Wb/m2B3×10−8Wb/m2C2×10−8Wb/m2D5.5×10−8Wb/m2Magnetic field at a distance r from an infinitely long straight conductor carrying steady varies as
Aμ04π2IrBμ04πIrCμ0IπrD2μ0Iπr
A wire of length 3 cm has current 1 amp. Find magnetic field at a perpendicular distance a cm from centre of wire

View SolutionThe magnitude of magnetic field at a point having perpendicular distance 50 mm from a long straight conducting wire carrying a current of 3A is
View SolutionA long, straight wire carries a current i. Let B_1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section. Let B_2 be the magnetic field at this point due to this section only. Find the value of d/l so that B_2 differs from B_1 by 1 %.
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)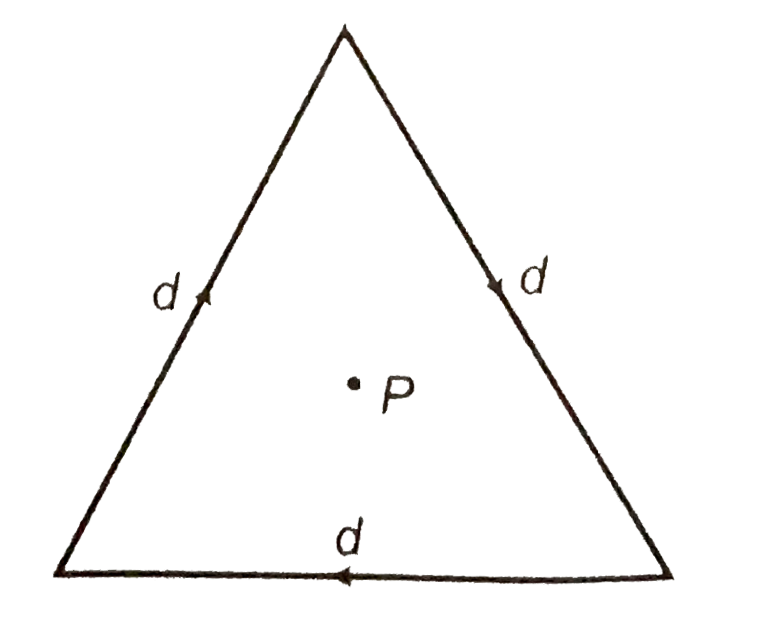
P is the centre of equilateral triangle.
(d)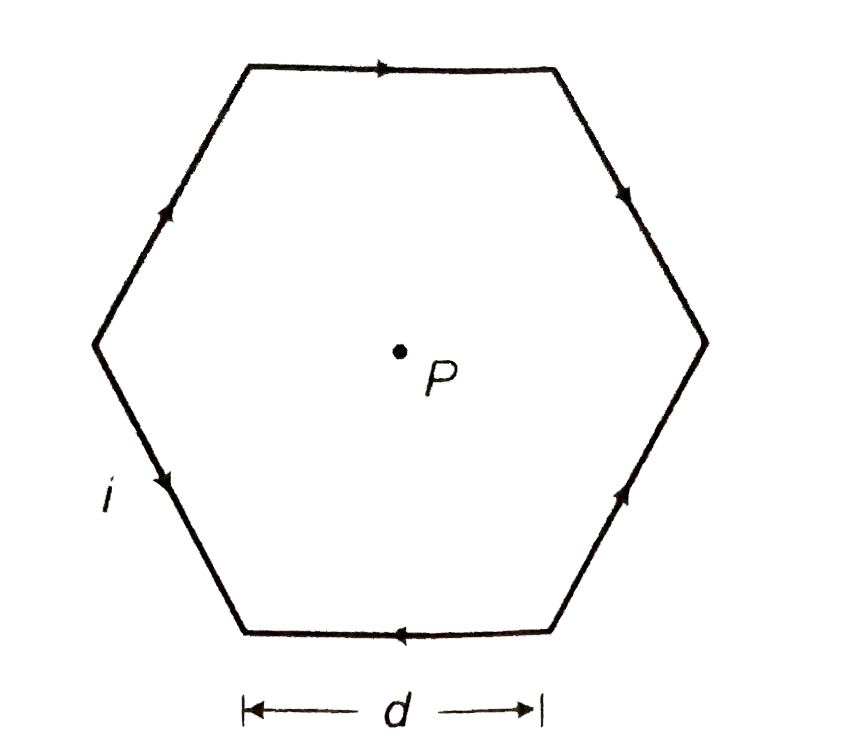
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)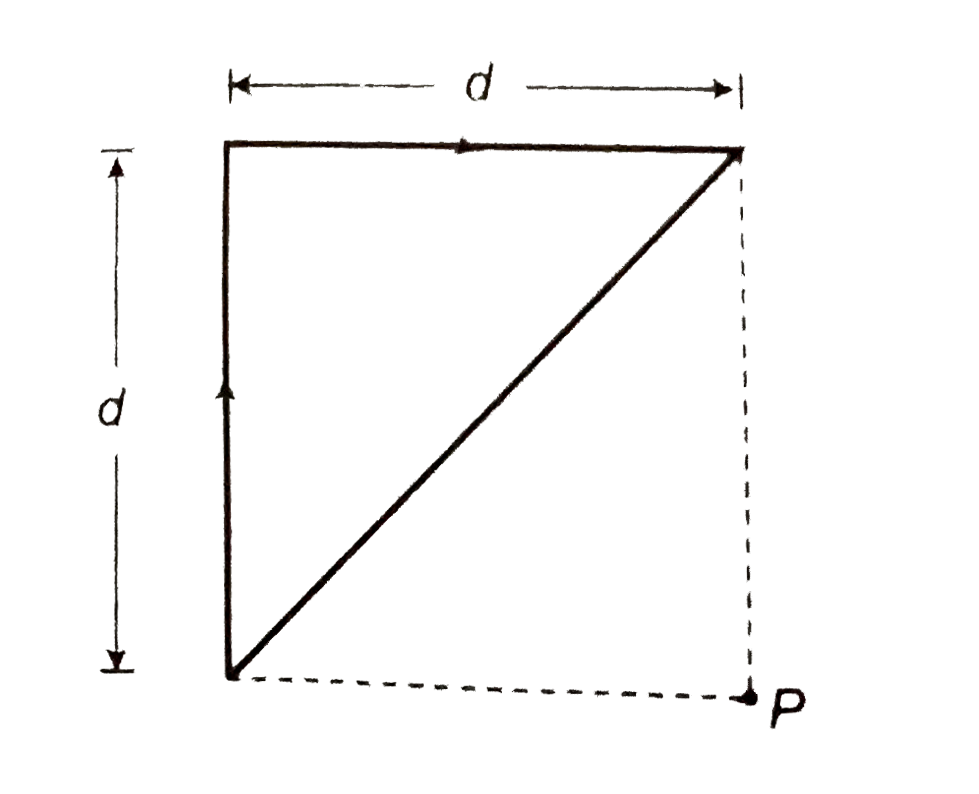
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionA wire of length 1 metre carrying a current of I ampere is bent in the form of a circle. Magnitude of its magnetic moment will be
View Solution