A charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle with the field. The frequency of revolution of the particle
Depends on the angle
Is independent of the angle
Is proportional to the specific charge q/m of the particle
Is inversely proportional to the value of B
The correct Answer is:B, C, D
To find the frequency of revolution of a charged particle moving in a magnetic field at an angle θ, we can follow these steps:
Step 1: Understand the motion of the charged particle
When a charged particle with charge q and mass m enters a magnetic field of induction B at an angle θ, it experiences a magnetic force that acts perpendicular to its velocity. This force causes the particle to move in a circular path.
Step 2: Determine the effective velocity component
The velocity v of the charged particle can be decomposed into two components:
- The component parallel to the magnetic field: v∥=vcos(θ)
- The component perpendicular to the magnetic field: v_{\perpendicular} = v \sin(\theta)
Only the perpendicular component contributes to the circular motion in the magnetic field.
Step 3: Apply the formula for the frequency of revolution
The frequency f of the circular motion of a charged particle in a magnetic field is given by the formula:
f=qB2πm
However, since only the perpendicular component of the velocity contributes to the circular motion, we need to consider the effective velocity v_{\perpendicular}.
Step 4: Relate the frequency to the perpendicular velocity
The centripetal force required for circular motion is provided by the magnetic force:
F = qv_{\perpendicular}B
The centripetal force can also be expressed as:
F = \frac{mv_{\perpendicular}^2}{r}
Setting these two expressions for force equal gives:
qv_{\perpendicular}B = \frac{mv_{\perpendicular}^2}{r}
From this, we can derive the radius r of the circular path:
r = \frac{mv_{\perpendicular}}{qB}
Step 5: Calculate the frequency using the effective velocity
Now, substituting v_{\perpendicular} = v \sin(\theta) into the frequency formula:
f=qB2πm⋅vsin(θ)r
Since the radius r is already expressed in terms of v_{\perpendicular}, we can simplify the expression for frequency:
f=qBsin(θ)2πm
Final Expression
Thus, the frequency of revolution of the charged particle in the magnetic field at an angle θ is given by:
f=qBsin(θ)2πm
---
When a charged particle with charge q and mass m enters a magnetic field of induction B at an angle θ, it experiences a magnetic force that acts perpendicular to its velocity. This force causes the particle to move in a circular path.
The velocity v of the charged particle can be decomposed into two components:
- The component parallel to the magnetic field: v∥=vcos(θ)
- The component perpendicular to the magnetic field: v_{\perpendicular} = v \sin(\theta)
The frequency f of the circular motion of a charged particle in a magnetic field is given by the formula:
f=qB2πm
However, since only the perpendicular component of the velocity contributes to the circular motion, we need to consider the effective velocity v_{\perpendicular}.
The centripetal force required for circular motion is provided by the magnetic force:
F = qv_{\perpendicular}B
The centripetal force can also be expressed as:
F = \frac{mv_{\perpendicular}^2}{r}
Setting these two expressions for force equal gives:
qv_{\perpendicular}B = \frac{mv_{\perpendicular}^2}{r}
From this, we can derive the radius r of the circular path:
r = \frac{mv_{\perpendicular}}{qB}
Now, substituting v_{\perpendicular} = v \sin(\theta) into the frequency formula:
f=qB2πm⋅vsin(θ)r
Since the radius r is already expressed in terms of v_{\perpendicular}, we can simplify the expression for frequency:
f=qBsin(θ)2πm
Thus, the frequency of revolution of the charged particle in the magnetic field at an angle θ is given by:
f=qBsin(θ)2πm
Topper's Solved these Questions
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Linked Comprehension)
2 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Matrix - Match)
2 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Single correct Choice Type )
24 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Practice Question (Integer Type)
4 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
Similar Questions
Motion of a charged particle in a uniform magnetic field |Questions
View SolutionA positive charge particle of charge q and mass m enters into a uniform magnetic field with velocity v as shown in Fig. There is no magnetic field to the left of PQ. Find (a) time spent, (b) distance travelled in the magnetic field, (c) impulse of magnetic force.

View Solution
Knowledge Check
A particle of charge q and mass m, is fired perpenducular to a magnetic field (B) with a velocity v. What is the frequency of revolution of the particle?
A2πBqB2πBqmC2πmBqDBq2πmA charged particle of mass m and charge q describes circular motion of radius r in a uniform magnetic field of strength B. The frequency of revolution is
A3Bq2πmB3Bq2πmC2πm2BqDBq2πmA charged particle of mass m and charge q is projected into a uniform magnetic field of induciton →B with speed v which is perpendicular to →B. The width of the magnetic field is d. The impulse imparted to the particle by the field is (d<<mv/qB)
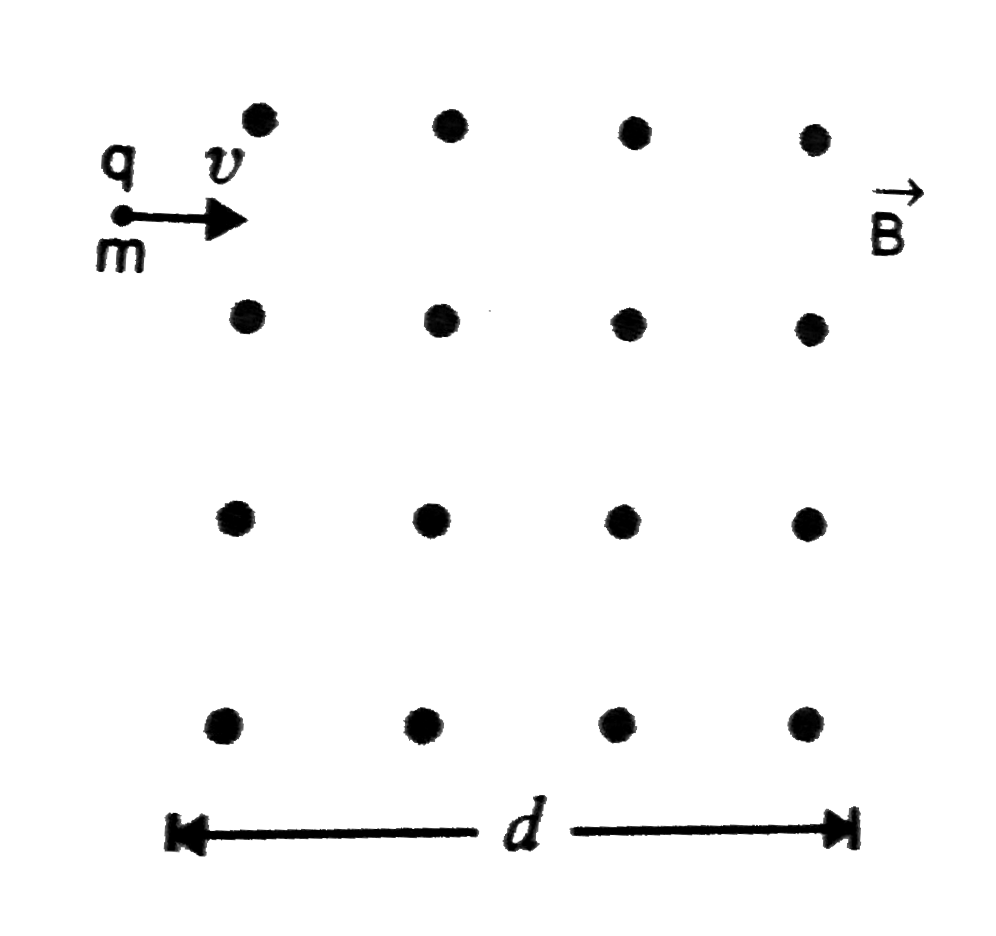 AqBdBqBv/dCmv/(qBd)Dmv2/(qBd)
AqBdBqBv/dCmv/(qBd)Dmv2/(qBd)
A particle of charge q and mass m is prjected in a uniform and contant magnetic field of strength B.The initial velocity →v makes angle θ with the →B.Find the distance travelled by the particle in time t.
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA charged particle of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius fo the resulting path is
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle E, then frequency of rotation is
View SolutionIf a charge particle of charge q , mass m , moves in a circular path in magnetic field of induction B , under a potential of V volts then radius of circular path is
View Solution
