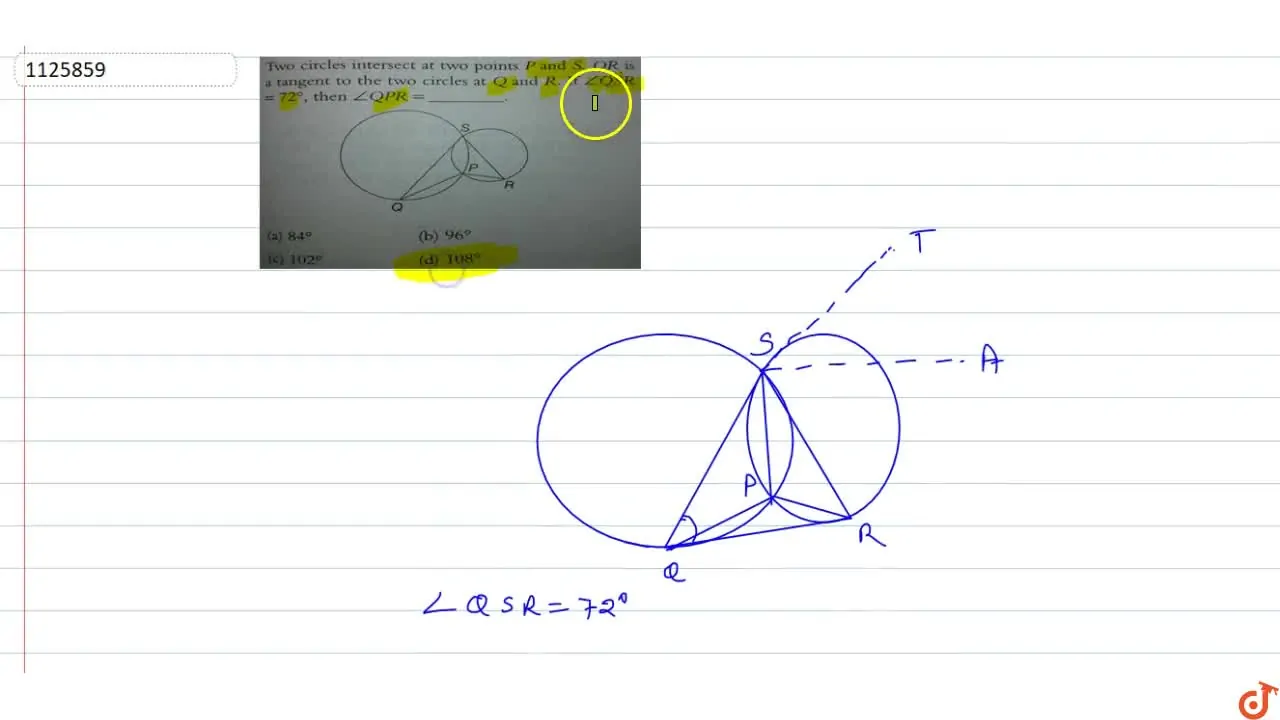
Two circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
84∘
96∘
102∘
108∘
The correct Answer is:D
(i) Apply 'alternate segment theorem'
(ii) Join QR and join PS.
∠PQR=∠PSQ and
∠PRQ=∠PSR (By alternate segment theorem)
Related Playlists
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -315videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -134videos
GEOMETRY
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 310videos
BANKING
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-315videos
LIMITS
Similar Questions
Two circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
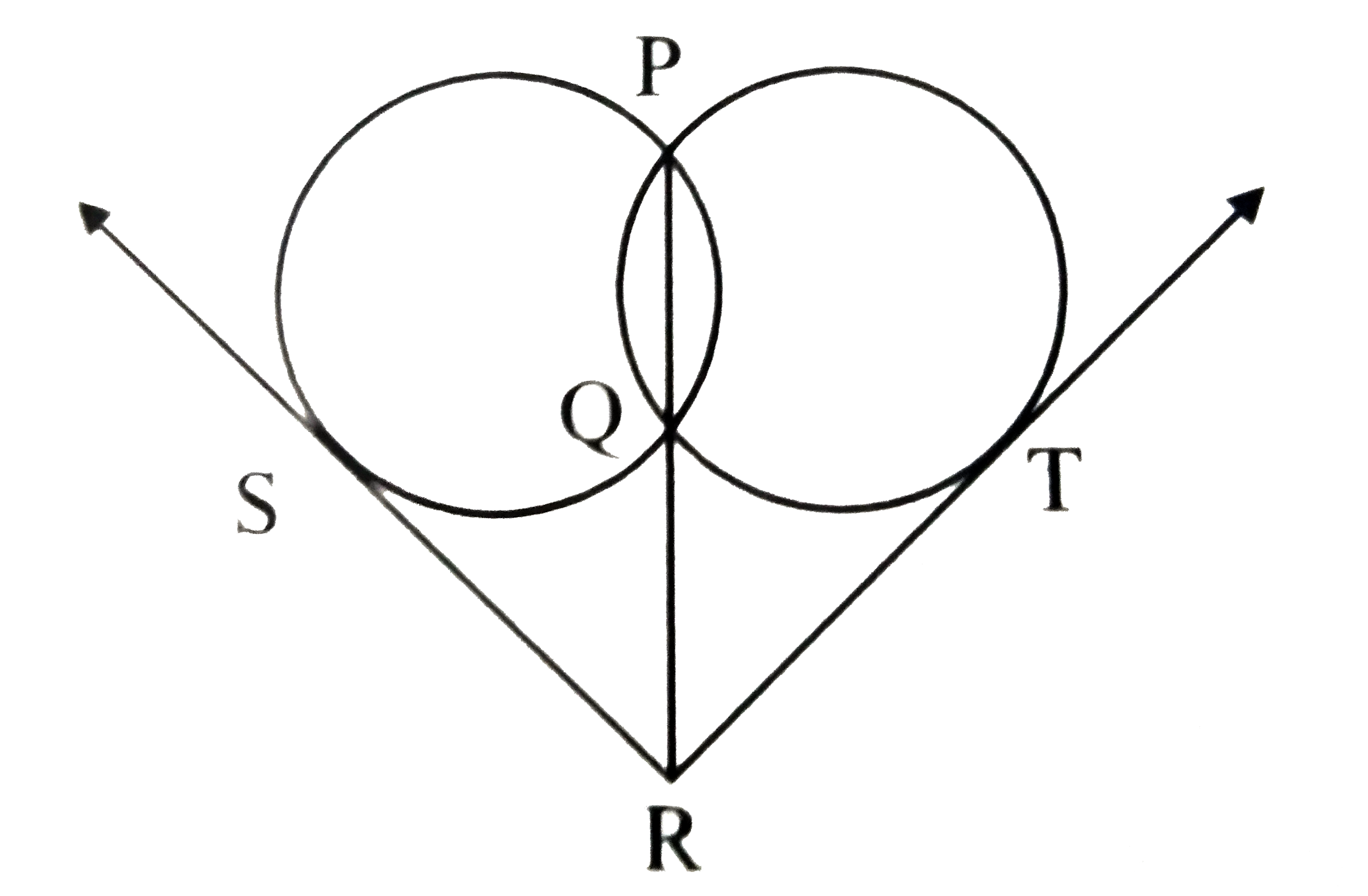
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
 View Solution
View SolutionTwo circles intersect each other at point P an Q. If PA and PB are two diameter then find ∠AQB.
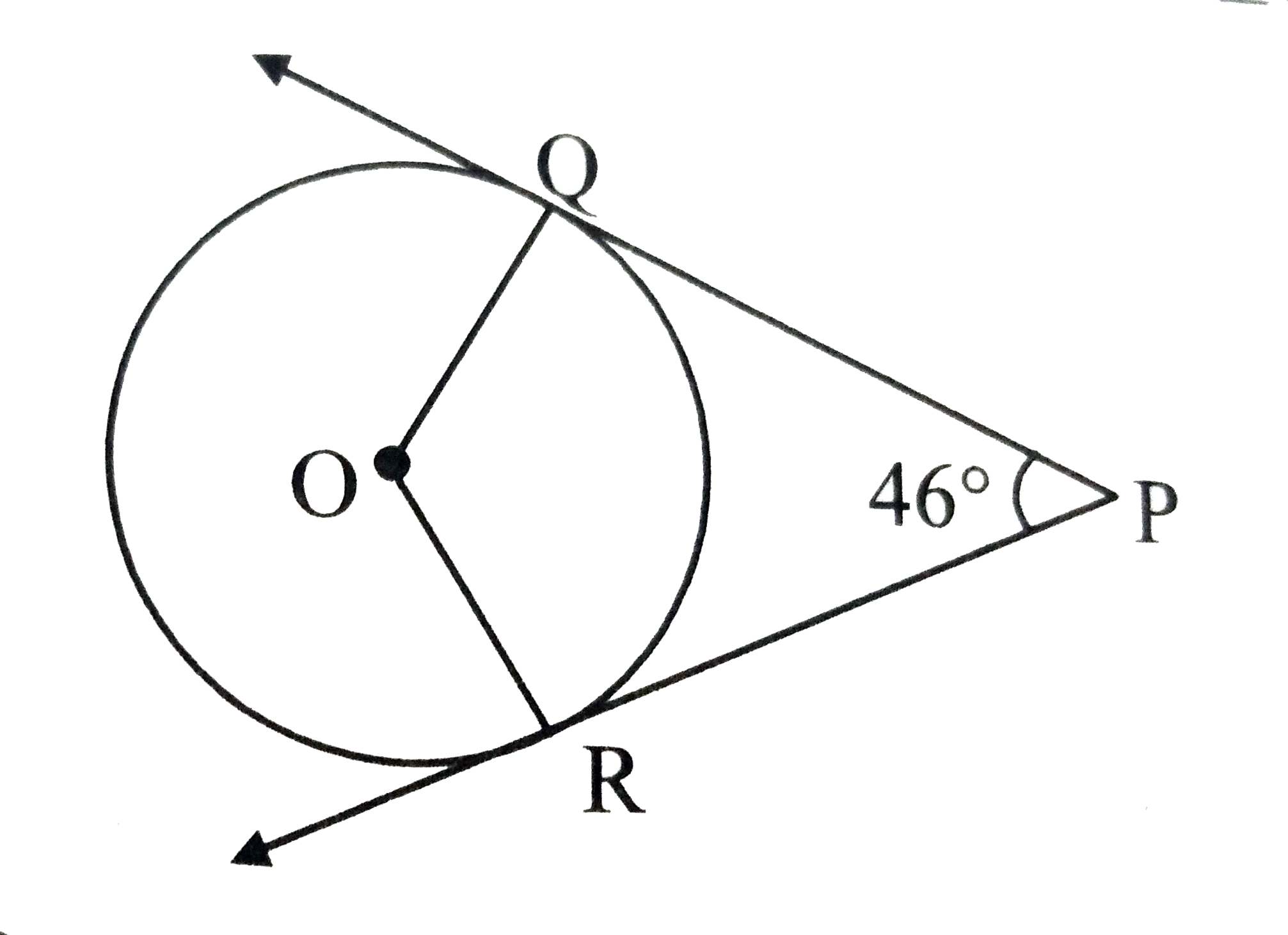
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals
 View Solution
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm , respectively intersect at two points P and Q such that OP and O'P are tangents to the two circle . Find the length of the common chord PQ.
View SolutionTwo circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionTwo circles intersect each other at P and Q. PA and PB are two diameters. Then ∠AQB is
View SolutionTwo circles touch each other externally at point A and PQ is a direct tangent which touch circle at P and Q respectively then ∠PAQ = ?
View SolutionTwo circles with centres A and B of radii 3 cm and 4 cm respectively intersect at two points C and D, such that AC and BC are tangents to the two circle. Find the length of the common chord CD.
View Solution