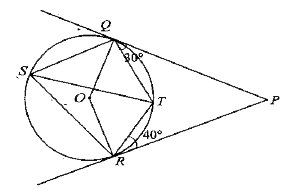
In the figure above (not to scale), PQ is a tangent segment to the circle at P.If P,R,S and T are concyclic points, ∠QPR=40∘ and PR=RQ then find ∠PTS.
80∘
100∘
60∘
120∘
The correct Answer is:B
Given PR=RQand∠Q=40∘
⇒∠RPQ=∠Q
∴∠RPQ=40∘
In ∠PQR,
∠PRQ=180∘−(40∘+40∘)=100∘.
We have, exterior angle of cyclic qudarilateralis equal to its interior opposite angle.
∴∠PTS=∠PRQ
(∵PRST "a cyclic quadrilateral")
∴∠PTS=100∘.
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -1
34 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Knowledge Check
PQ is a tangent to the circle at T. If TR = TS where R and S are points on the circle and ∠RST=65∘, the ∠PTS =
A65∘B130∘C115∘D55∘PQ is tangent at a point R of the circle with centre O. If ST is a diameter of the circle and ∠TRQ=30∘ find ∠PRS
A30∘B60∘C45∘D120∘
In the figure above, ∠SPT=60∘and PQ=PR. Find ∠PQRA50∘B45∘C60∘D55∘
In the figure below (not to scale), PQ=PR=8cm and O is the centre of the circle . If each of the chords PQ and PR makes an angle of 120∘ at the centre of the circle , then find the area of the shaded region .
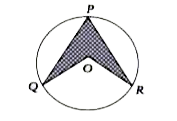
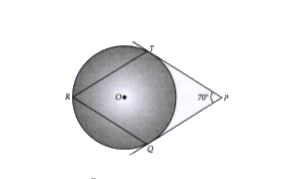
View SolutionIn figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ=70∘, find ∠TRQ.
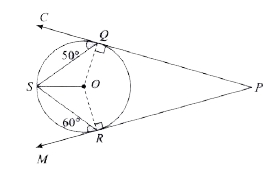
View SolutionIn the figure , PQ and PR are tangent to the circle with centre O. Also, S is a point on the circle such that ∠SQC=50∘and∠SRM=60∘, then ∠QSR=
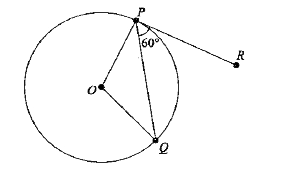
View SolutionIn figure PR is tangent to the circle at P and O is the centre of the circle. The value of ∠POQ is
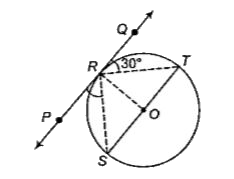
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
View Solution