In the following figure, O is the centre of the circle , AC is the diameter and if ∠APB=120∘ , then find ∠BQC .
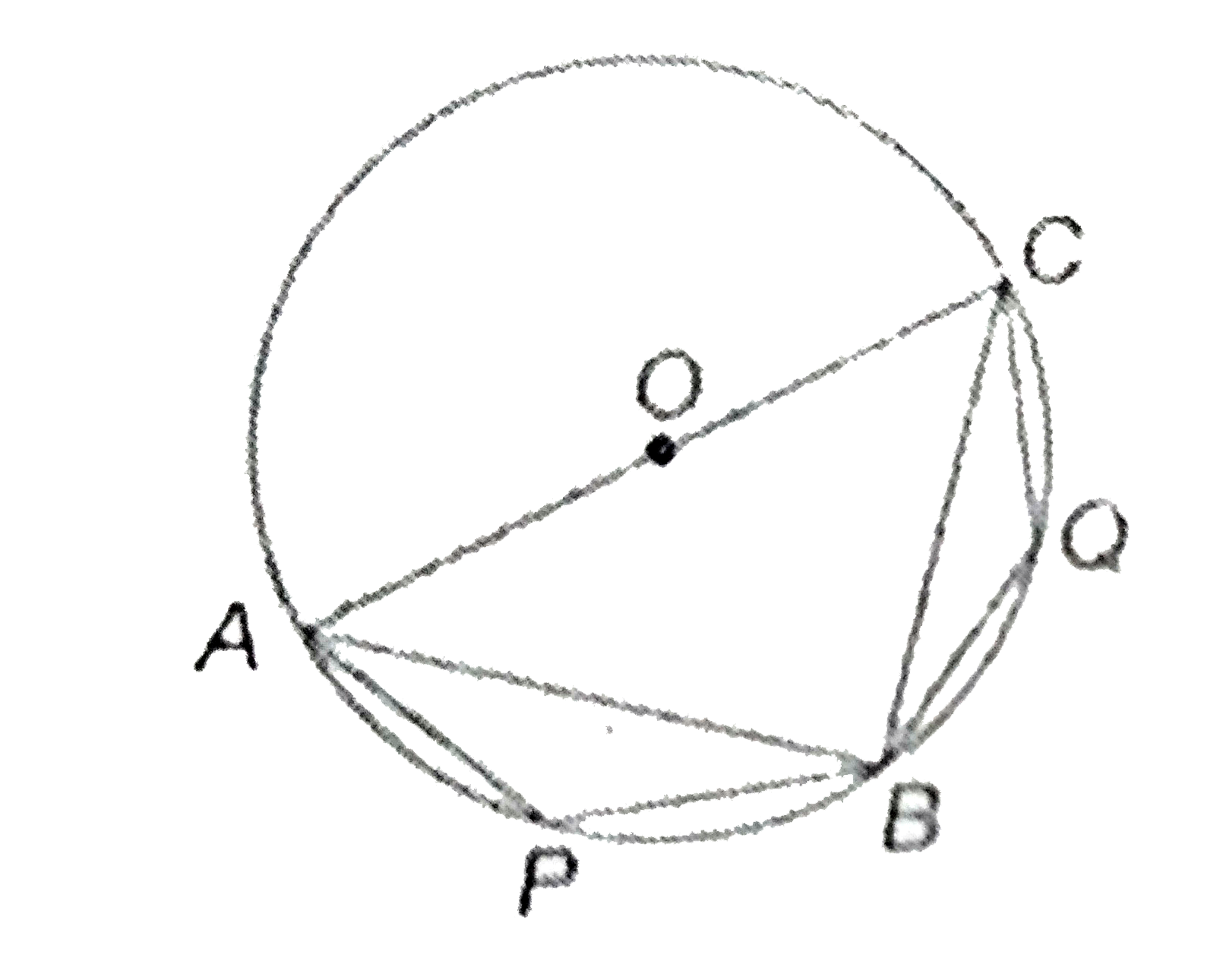
A
30∘
B
150∘
C
90∘
D
120∘
Video Solution
Text Solution
The correct Answer is:B
(i) APBC is a cyclic quadrilateral.
(ii) ∠ABC is an angle in a semi circle.
(iii) ABQC is a cyclic quadrillteral.
|
Topper's Solved these Questions
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -3
15 Videos
- GEOMETRYBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRYEXERCISE - Concept Application Level -1
34 Videos
- BANKING BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - BANKING EXERCISE - LEVEL 3
10 Videos
- LIMITSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIMITSEXERCISE - LEVEL-3
15 Videos
Similar Questions
Knowledge Check
In the figure, O is the centre of the circle . ∠PQR is equal to
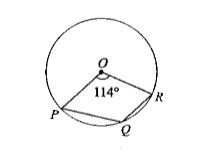 A57∘B63∘C123∘D92∘
A57∘B63∘C123∘D92∘If O is the centre of the circle then find ∠ADC
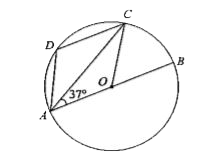 A125∘B127∘C90∘D137∘
A125∘B127∘C90∘D137∘
In the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
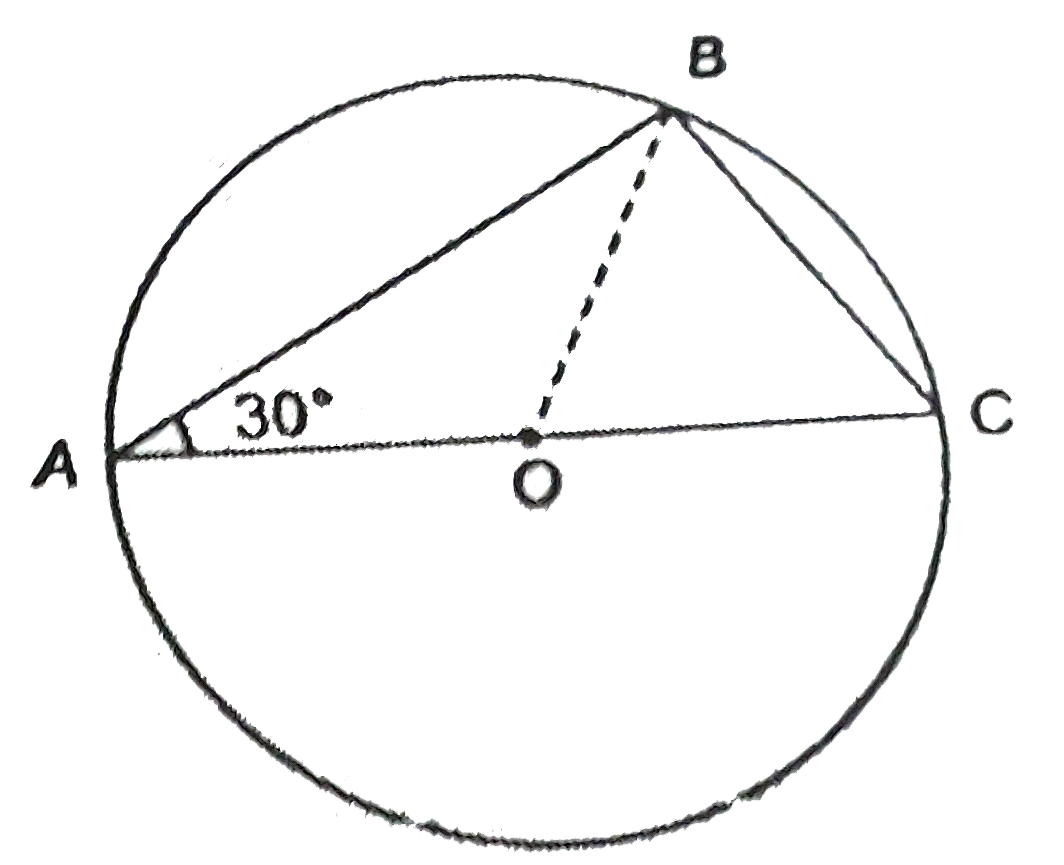
View SolutionIn the following figure, O is the centre of the circle. AB is an arc of the circle, such that ∠AOB=80∘.Find ∠ACB.
View SolutionIn the following figure, O is the centre of the circle. AB and CD are equal chords. If ∠AOB=100∘ , Find the ∠CED.

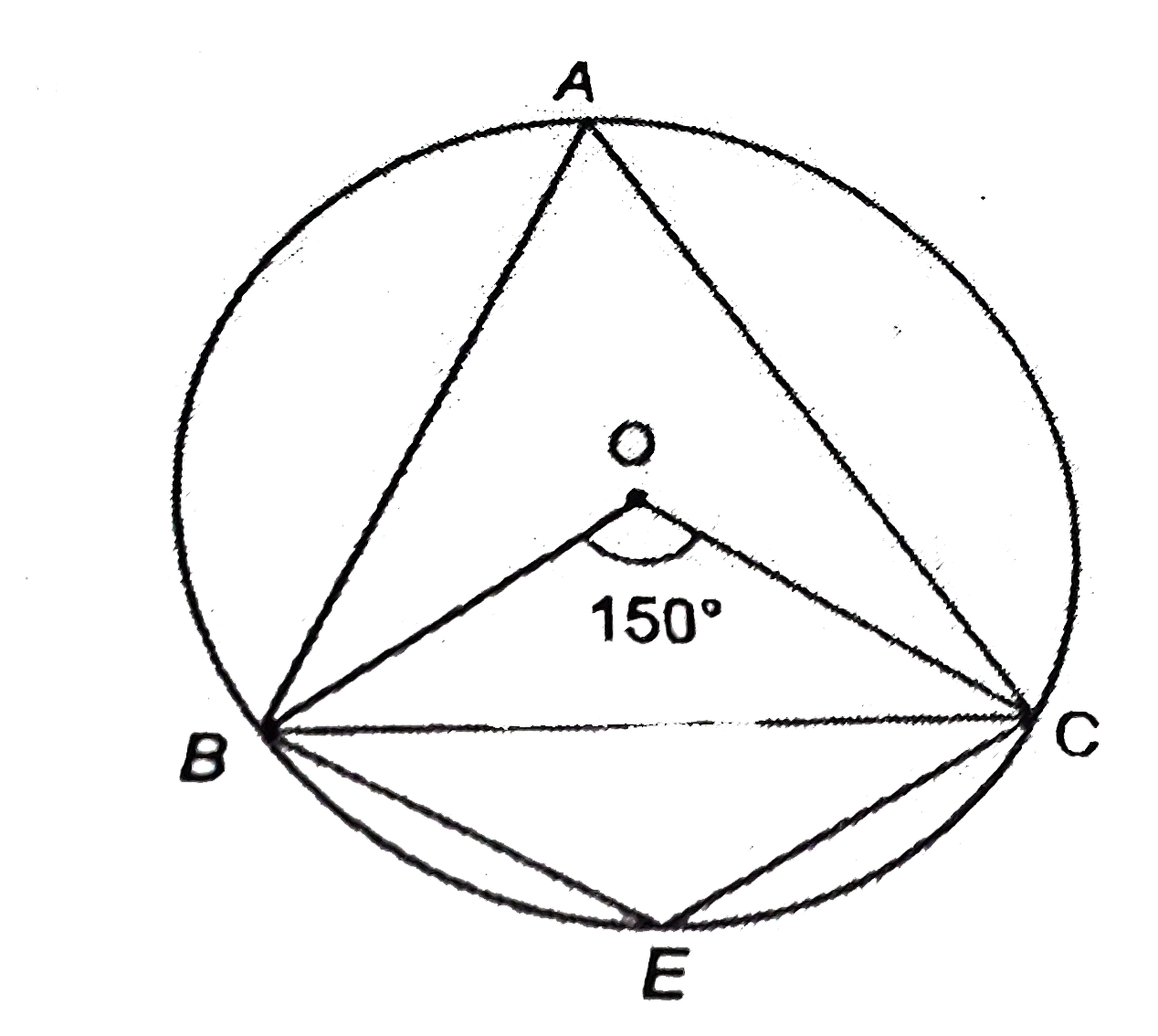
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
View SolutionIn the following figure, O is the centre of the circle. If ∠BAC=60∘ , then ∠OBC= __________

View SolutionIn the following figure, O is the centre of the circle and ∠AMB=120∘ , Find the angle between the two tangents AP and BP.

View Solution
