Distance of origin from the line (1+√3)y+(1−√3)x=10 along the line y=√3x+k (1) 2√5 (2) 5√2+k (3) 10 (4) 5
A
5√2
B
5sqrt(2)+k
C
10
D
5
Video Solution
Text Solution
The correct Answer is:D
Slope of the line L≡(1+√3)y+(1−√3)x=10 is
√3−1√3+1=tan15∘.
Slope of line y=√3x+k is √3=tan60∘.
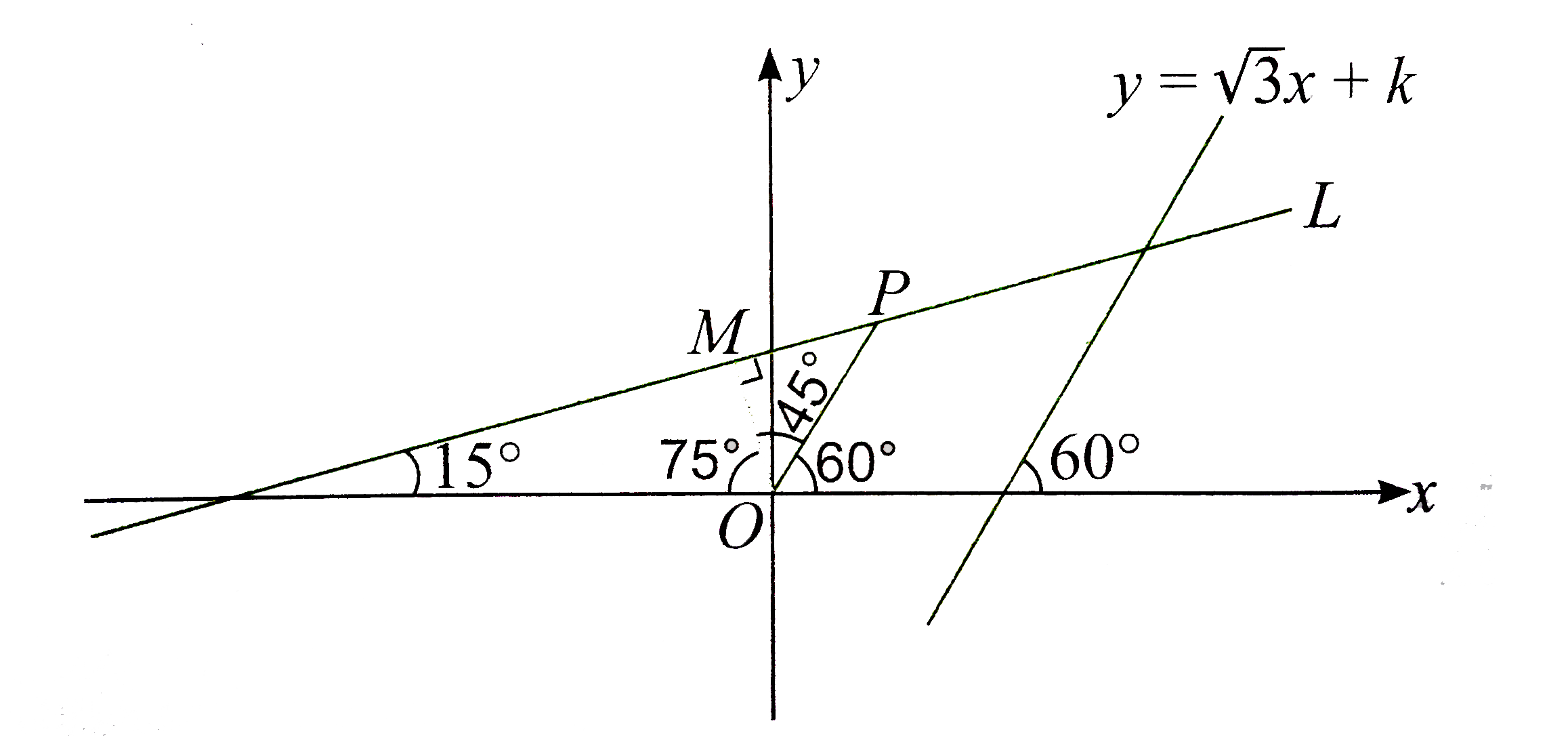
In the figure, distance of origin from line L measured along the line y=√3x+k is OP.
From the figure.
OP=OMsec45∘
=|0+0−10|√(√3−1)2+(√3+1)2√2=10√8√2=5
|
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Knowledge Check
For which of the following curves, the line x+√3y=2√3 is the tangent at the point (3√32,12) ?
Ax2+y2=7By2=16√3xC2x2−18y2=9Dx2+9y2=9The angle between the lines y=(2−√3)X+5andy=(2+√3)X−7 is
A30∘B60∘C45∘Dtan−13What is the angle between the two straight lines y=(2−√3)x+5 and y=(2+√3)x−7 ?
A60∘B45∘C30∘D15∘
The distance of the point (1,−5,9) from the plane x−y+z=5 measured along a straighat line x=y=z is (A) 5√3 (B) 3√10 (C) 3√5 (D) 10√3
View SolutionThe distance of the point (1, 2, 3) from the plane x+y−z=5 measured along the straight line x=y=z is 5√3 (2) 10√3 (3) 3√10 3√5 (5) 2√5
View Solutionif x=√3+1√3 and y=√3−1√3 thenx2−y2 is
View SolutionThe point, at shortest distance from the line x+y=10 and lying on the ellipse x2+2y2=6, has coordinates (A) (√2,√2) (B) (0,√3) (C) (2,1) (D) (√5,1√2)
View SolutionFind the angle between the lines y=(2−√3)(x+5) and y=(2+√3)(x−7).
View Solution
