are the variable points of the y-axis such that lies below . Lines intersect at The locus of is
The correct Answer is:D
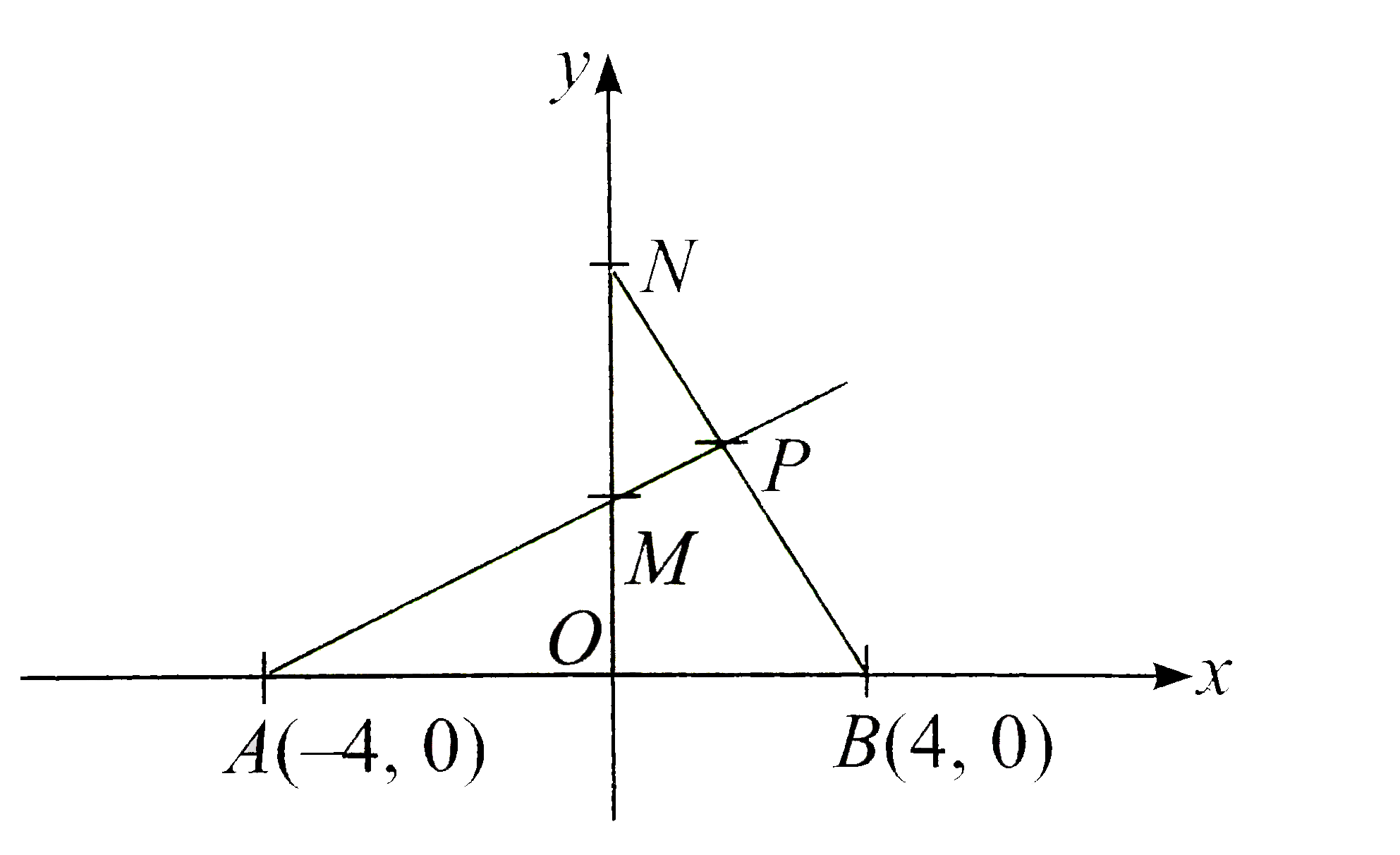
The equation of AM is
The equation of BN is
(Eliminating h)
which is the required locus
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)
30 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)
27 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.6
5 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
A≡(−4,0),B≡(4,0) M and N are the variable points of the y-axis such that M lies below N and MN=4 . Lines AMandBN intersect at P. The locus of P is (a) 2xy−16−x2=0 (b)2xy+16−x2=0 (c) 2xy+16+x2=0 (d)2xy−16+x2=0
View SolutionFind the coordinates of the point of intersection of the lies 2x−y+3=0 and x+2y−4=0.
View Solution
Knowledge Check
x2−16=0,y2−9y+20=0
Aif x>yBif x≥yCif x<yDif x≤yLet (x,y) be any point on the parabola y2=4x. Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
Ax2=yBy2=2xCy2=xDx2=2yThe radical centre of the circles
x2+y2−16x+60=0
x2+y2−12x+27=0 and x2+y2−12y+8=0 isA(13,334)B(334,−13)C(334,13)DNone of these
A line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. Image of the locus of R in the line y=−x is : (A) x2+y2−2x+4y=0 (B) x2+y2+2x+4y=0 (C) x2+y2−4y=0 (D) x2+y2+2x−4y=0
View SolutionA line intersects x-axis at A(2,0) and y-axis at B(0,4). A variable lines PQ which is perpendicular to AB intersects x-axis at P and y-axis at Q. AQandBP intersect at R. Locus of R is : (A) x2+y2−2x+4y=0 (B) x2+y2+2x+4y=0 (C) x2+y2−2x−4y=0 (D) x2+y2+2x−4y=0
View SolutionFind the acute angle between the lines 2x−y+3=0 and x+y+2=0.
View Solutiony=mx be a variable line (m is variable) intersect the lines 2x+y−2=0 and x−2y+2=0 in P and Q.The locus of midpoint of segment of PQ is
View SolutionI. x2+4x+4=0
II. y2−8y+16=0
View Solution
