A triangle is formed by the lines $x + y = 0, x - y = 0,$ and $l x + m y = 1 .$ If $l a n d m$ vary subject to the condition $l^{2} + m^{2} = 1,$ then the locus of its circumcenter is ${(x^{2} - y^{2})}^{2} = x^{2} + y^{2}$ ${(x^{2} + y^{2})}^{2} = (x^{2} - y^{2})$ ${(x^{2} + y^{2})}^{2} = 4 x^{2} y^{2}$ ${(x^{2} - y^{2})}^{2} = {(x^{2} + y^{2})}^{2}$

A

${(x^{2} - y^{2})}^{2} = x^{2} + y^{2}$

B

${(x^{2} - y^{2})}^{2} = (x^{2} - y^{2})$

C

$(x^{2} - y^{2}) = 4 x^{2} y^{2}$

D

${(x^{2} - y^{2})}^{2} = {(x^{2} + y^{2})}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The coordinates of circumcenter are $(l / (l^{2} - m^{2}), m / (m^{2} - l^{2})) .$
Hence,
$h = \frac{l}{l^{2} - m^{2}} (1)$
$k = - \frac{m}{l^{2} - m^{2}} (2)$

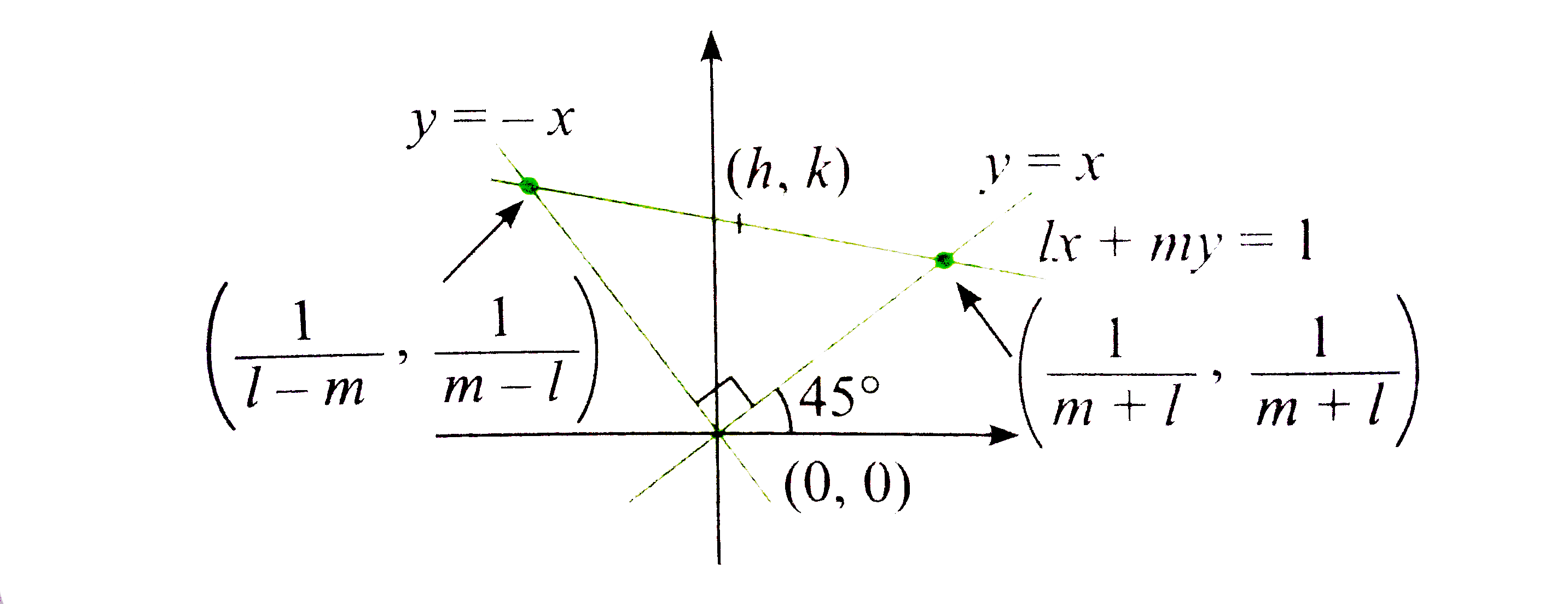
Squaring and adding (1) and (2), we get
$h^{2} + k^{2} = \frac{l^{2} + m^{2}}{{(l^{2} - m^{2})}^{2}} = \frac{1}{{(l^{2} - m^{2})}^{2}} (Putting l^{2} + m^{2} = 1)$
$Also, h^{2} - k^{2} = \frac{1}{l^{2} - m^{2}}$
Therefore, the locus is $x^{2} + y^{2} = {(x^{2} - y^{2})}^{2}$ .

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A triangle is formed by the lines $x + y = 0, x - y = 0 and l x + m y + 1 = 0$ . If l and m vary subject to the condition $l^{2} + m^{2} = 1$ , then the locus of the circumcentre of the triangle is
A ${(x^{2} - y^{2})}^{2} = x^{2} + y^{2}$
B ${(x^{2} + y^{2})}^{2} = x^{2} - y^{2}$
C $x^{2} + y^{2} = 4 x^{2} y^{2}$
D ${(x^{2} - y^{2})}^{2} = {(x^{2} + y^{2})}^{2}$
Question 2 - Select One
Area of triangle formed by straight lines $x + y = 4, 2 x - y = 2 and x - 2 = 0$ is
A4 sq. unit
B9 sq. unit
C $\frac{7}{2}$ sq. unit
DNone of these
Question 3 - Select One
The value of $\frac{x + y}{x - y} + \frac{x - y}{x + y} - \frac{2 (x^{2} - y^{2})}{x^{2} - y^{2}}$ is :
A $1$
B $x$
C $y$
D $0$

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile