The equation of the bisector of the acute angle between the lines $2 x - y + 4 = 0$ and $x - 2 y = 1$ is $x - y + 5 = 0$ $x - y + 1 = 0$ $x - y = 5$ (d) none of these

A

x+y+5=0

B

x-y+1=0

C

x-y=5

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

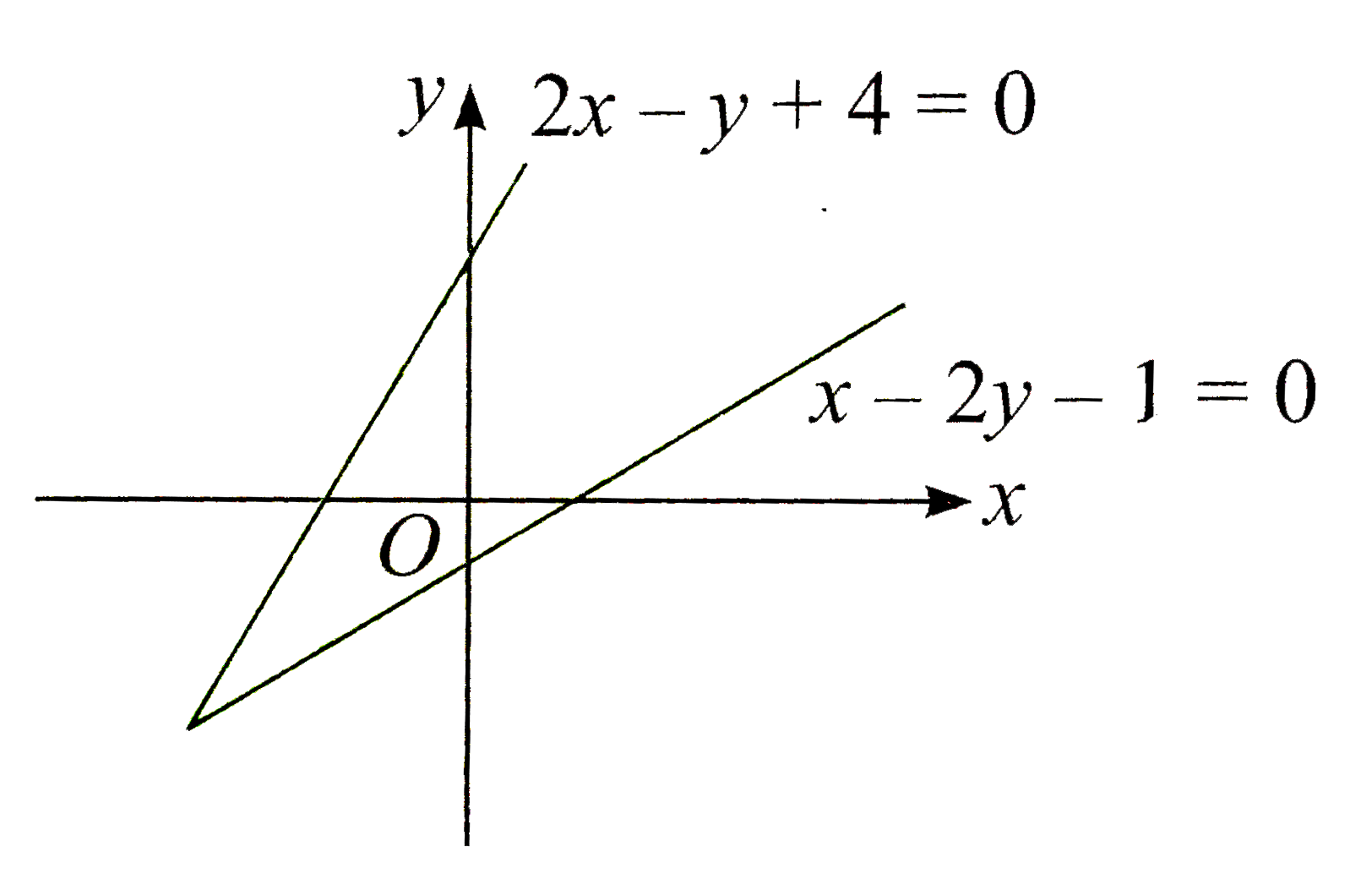
Clearly, from the figure, the origin is contained in the acute angle. Writing the equations of thel lines as 2x-y+4=0 and -x+2y+1=0, the required bisector is
$\frac{2 x - y + 4}{\sqrt{5}} = \frac{- x + 2 y + 1}{\sqrt{5}}$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The equation of the bisector of the acute angle between the lines
$3 x - 4 y + 7 = 0$ and $12 x + 5 y - 2 = 0$ is
A(a) 21x + 77y - 101 = 0
B(b) 99x - 27y + 81 = 0
C(c) 21x - 77y + 101 = 0
D(d) None of the above
Question 2 - Select One
The equation of the bisector of the obtuse angle between the lines 3x-4y+7=0 and -12x-5y+2=0 is
A21x+77y+101=0
B21x+77y-101=0
C21x+77y=0
DNone of the above
Question 3 - Select One
Equation of the bisector of the acute angle between lines 3x+4y+5=0 and 12x-5y-7=0 is
A21x+77y+100=0
B99x-27y+30=0
C99x+27y+30=0
D21x-77y-100=0

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile