P is a point on the line y+2x=1, and QandR two points on the line 3y+6x=6 such that triangle PQR is an equilateral triangle. The length of the side of the triangle is 2√5 (b) 3√5 (c) 4√5 (d) none of these
2/√15
3/√5
4/√5
none of these
The correct Answer is:A
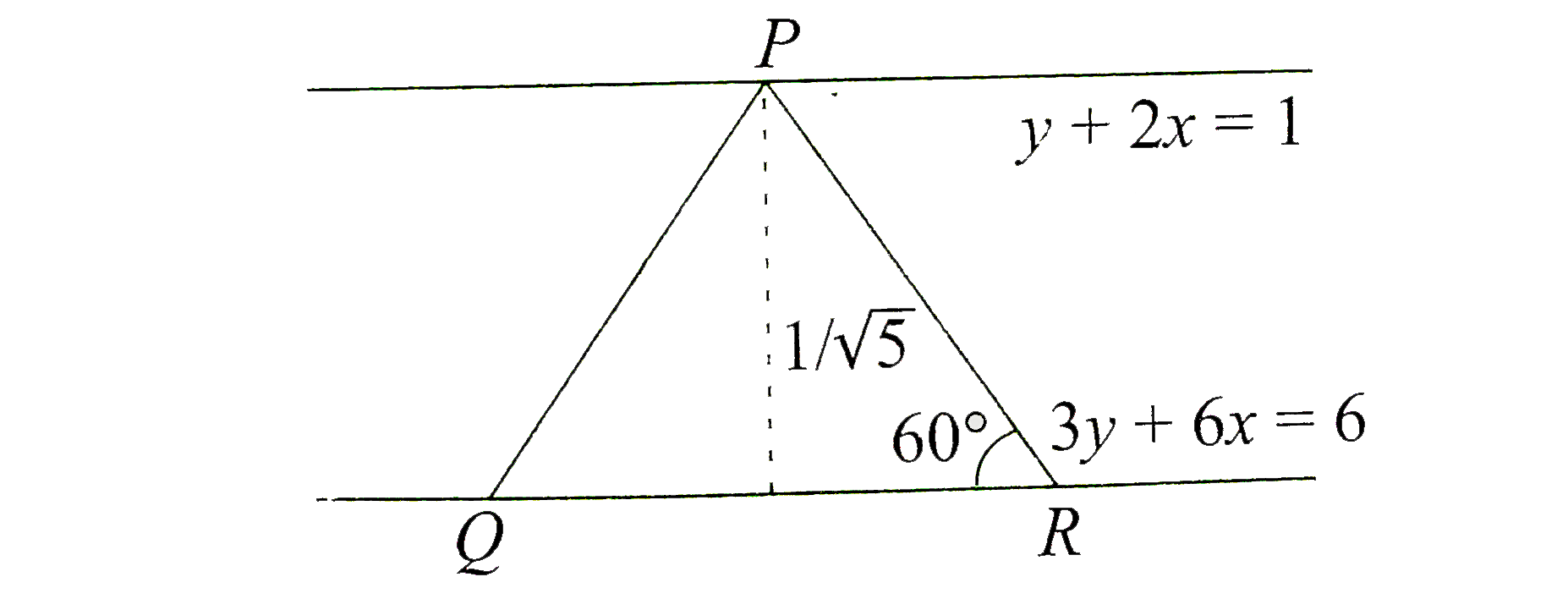
The given lines are y+2x=1 and y+2x=2. The distance between the lines is (2−1)/√5=1/√5.
The side length of the triangle is
1√5 cosec 60∘=2√15
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
P is a point on the line y+2x=1, and Q and R two points on the line 3y+6x=6 such that triangle PQR is an equilateral triangle. The length of the side of the triangle is 2√5 (b) 3√5 (c) 4√5 (d) none of these
View SolutionThe equation of the base of an equilateral triangle ABC is x+y=2 and the vertex is (2,−1) . The area of the triangle ABC is: √26 (b) √36 (c) √38 (d) None of these
View Solution
Knowledge Check
Let P is a point on the line y+2x=2 and Q and R are two points on the line 3y+6x=3. If the triangle PQR is an equilateral triangle, then its area (in sq. units) is equal to
A115B15√3C13√5D12√15Of the three lines x+√3y=0,x+y=1 and x−√3y=0 two are equations of two altitudes of an equilateral triangle. The centroid of Δ is the point
A(0,0)B(√3√3−1,1√3−1)C(√3√3+1,1√3+1)DNone of these
The line x+y=√6, forms an equilateral triangle with the lines x2−4xy+y2=0, The perimeter of the triangle is :
View SolutionIf the sides of a right-angled triangle are in A.P., then the sines of the acute angles are 35,45 b. 1√3,√23 c. 12,√32 d. none of these
View SolutionThe side of an equilateral triangle is 6√3 cm. Find the area of the triangle. [Take √3=1.732]
View SolutionThe lengths of the sides of a right triangle given by a (A) 1+√54,
(B) 1+√52
(C) 1+√5,
(D) 1−√52
View SolutionIf the equation of base of an equilateral triangle is 2x−y=1 and the vertex is (−1,2), then the length of the sides of the triangle is √203 (b) 2√15 √815 (d) √152
View SolutionFind the area of an equilateral triangle in which length of perpendicular on sides from a point D inside the Δ are 2√3+3√3and5√3
View Solution

