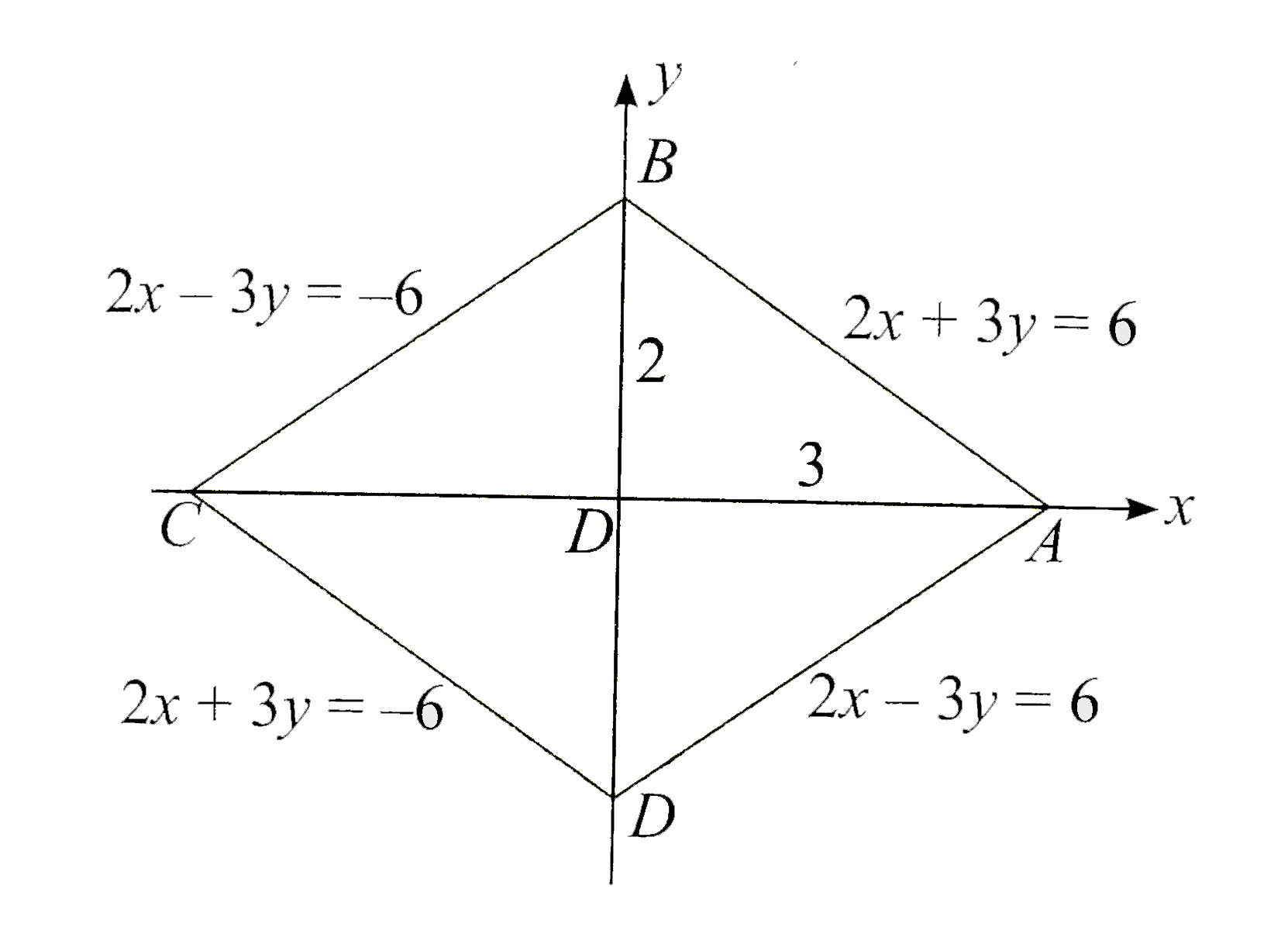
The are enclosed by $2 | x | + 3 | y | \leq 6$ is

A

3 sq. units

B

4 sq. units

C

12 sq. units

D

24 sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The given inequality is equivalent to the following system of inequalities.
$2 x + 3 y \leq 6, when x \geq 0, y \geq 0$
$2 x - 3 y \leq 6, when x \geq 0, y \leq 0$
$- 2 x + 3 y \leq 6, when x \leq 0, y \geq 0$
$- 2 x - 3 y \leq 6, when x \leq 0, y \leq 0$
which represents a rhombus with sides
$2 x \pm 3 y = 6 and 2 x \pm 3 y = - 6$
The lengths of the diagonals are 6 units and 4 units, respectively, along the x- and y-axes. Therefore, the required area is $1 / 2 \times 6 \times 4 = 12$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x + y) = f (x) f (y) \forall x, y \in R$ and $f (a) = 2$ then area enclosed by $3 | x | + 2 | y | \leq 8$ is:
Af (4) square units
B $\frac{1}{2} f (6)$ square units
C $\frac{1}{3} f (6)$ square units
D $\frac{1}{3} f (5)$ square units
Question 2 - Select One
The area enclosed by the corves $| y + x | \leq 1, | y - x | \leq 1$ and $2 x^{2} + 2 y^{2} = 1$ is
A $(2 + \frac{π}{2})$ sq units
B $(2 - \frac{π}{2})$ sq units
C $(3 + \frac{π}{2})$ sq units
D $(3 - \frac{π}{4})$ sq units
Question 3 - Select One
Statement I- The area by region $| x + y | + | x - y | \leq 2 is 4$ sq units. Statement II- Area enclosed by region $| x + y | + | x - y | \leq 2$ is symmetric about X-axis.
AStatement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
BStatement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I.
CStatement I is true , Statement II is false
DStatement I is false , Statement II is true

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile