The lien x3+y4=1 meets the y− and x−axys at AandB , respectively. A square ABCD is constructed on the line segment AB away from the origin. The coordinates of the vertex of the square farthest from the origin are (7, 3) (b) (4, 7) (c) (6, 4) (d) (3, 8)
7,3
4,7
6,4
3,8
The correct Answer is:B
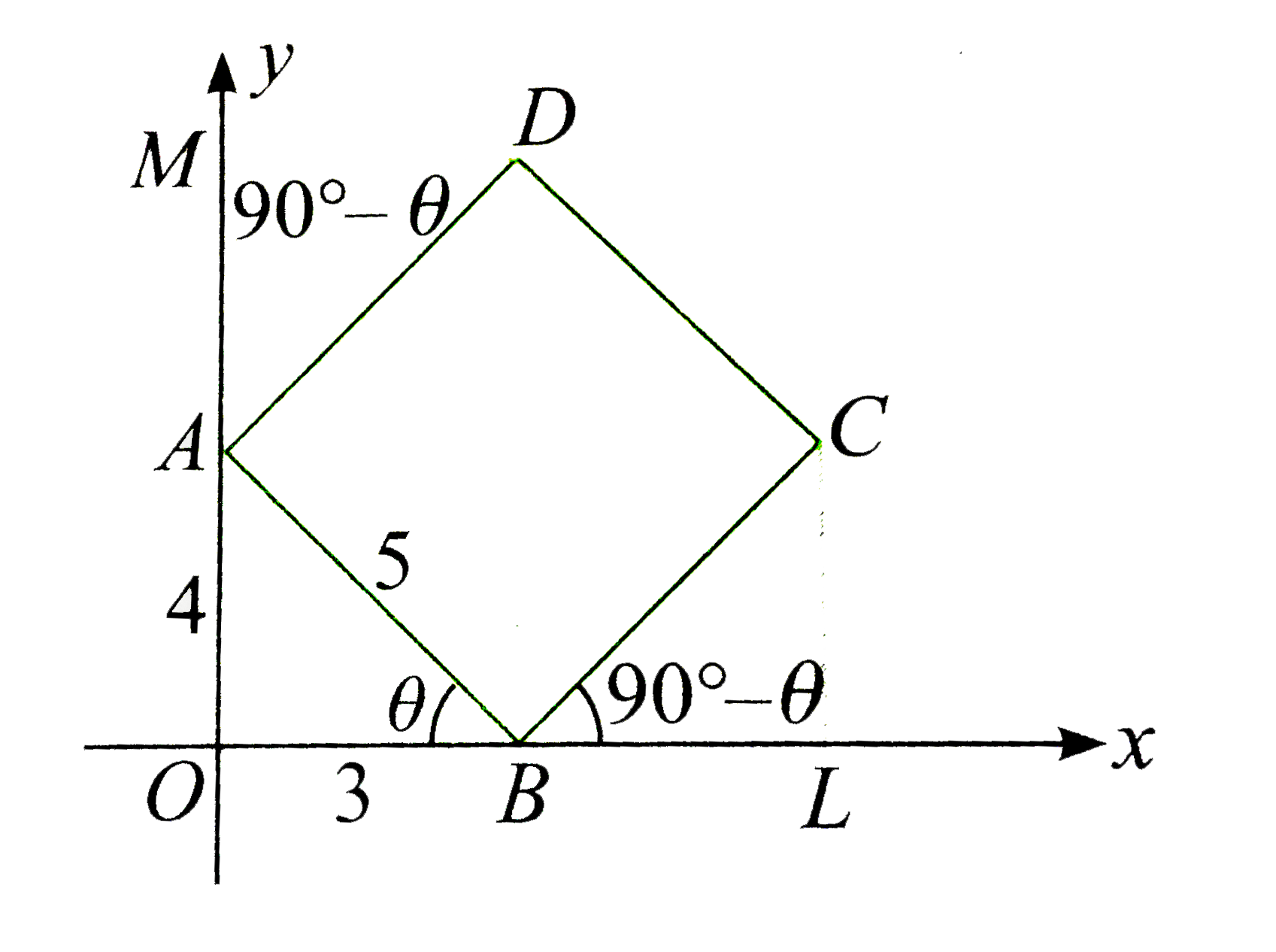
The coordinates of A are (0,4) and those of B are (3,0).
BC=AB=√32+42=5
or BL=BCsinθand CL=BCcosθ
or BL=5×45=4and
CL=5×35=3
Similarly, MD =4 and AM=3.
So, the coordinates of C are (OB+BL,CL) ≡(7,3) and those of D are (MD, OA+AM) ≡(4,7).
The coordinates of the vertex farthest from the origin are (4,7).
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Knowledge Check
On the portion of the line x3+y4=1 intercepted between the axes a square is constructed away from the origin. Coordinates of the vertex of square which is farthest from origin is
A(3,8)B(6,4)C(7,3)D(4,7)On the line joining the points A (0,4) and B (3,0), a square ABCD is constructed on the side of the line away from the origin. Equation of the circle having centre at C and touching the axis of x is
Ax2+y2−14x−6y+49=0Bx2+y2−14x−6y+9=0Cx2+y2−6x−14y+49=0Dx2+y2−6x−14y+9=0The vertices of a parallelogram in order are A(1, 2), B(4, y), C(x, 6), D(3, 5), then (x, y) =
A(6, 3)B(3, 6)C(5, 6)D(1, 4)
The distance of the point P(4, 3) from the origin is (a) 4 (b) 3 (c) 5 (d) 7
View SolutionThe distasnce of the plane 2x−3y+6z+14=0 from the origin is (A) 2 (B) 4 (C) 7 (D) 11
View SolutionThe line x+y=10 meets the y-axis at A and the x -axis at B .A square ABCD is constructed away from the origin with AB as a side.If the equation of CD is x+y=λ ,the value of λ is
View SolutionThe line x+y=p meets the x- and y-axes at AandB , respectively. A triangle APQ is inscribed in triangle OAB,O being the origin, with right angle at Q.P and Q lie, respectively, on OBandAB . If the area of triangle APQ is 38th of the are of triangle OAB, the AQBQ is equal to (a)2(b) 23 (c) 13 (d)3
View SolutionThe line y=3x4 meets the lines x−y+1−0 and 2x−y=5 at A and B respectively. Coordinates of P on y=3x4 such that PA⋅PB=25.
View Solution

