Evaluate : $[lim x \to 0 \frac{sin x}{x}]$ , where $[\cdot]$ represents the greatest integer function.

Video Solution

Text Solution

Verified by Experts

Let us first draw the graphs of y = x and y = sin x.
For y = x, y' = 1, i.e. the slope of line is 1 for all real x.
For y = sin x, y' = cos x.
Thus, both y = x and y = sin x have slope '1' at x = 0, hence the graphs touch each other at x = 0.
Moving from '0' to $' π / 2'$ , the values of cos x decrease from '1' to '0'.
Thus, the graph of y = sin x lies below the graph of y = x.
The graphs of y = x and y = sin x are plotted as follows.

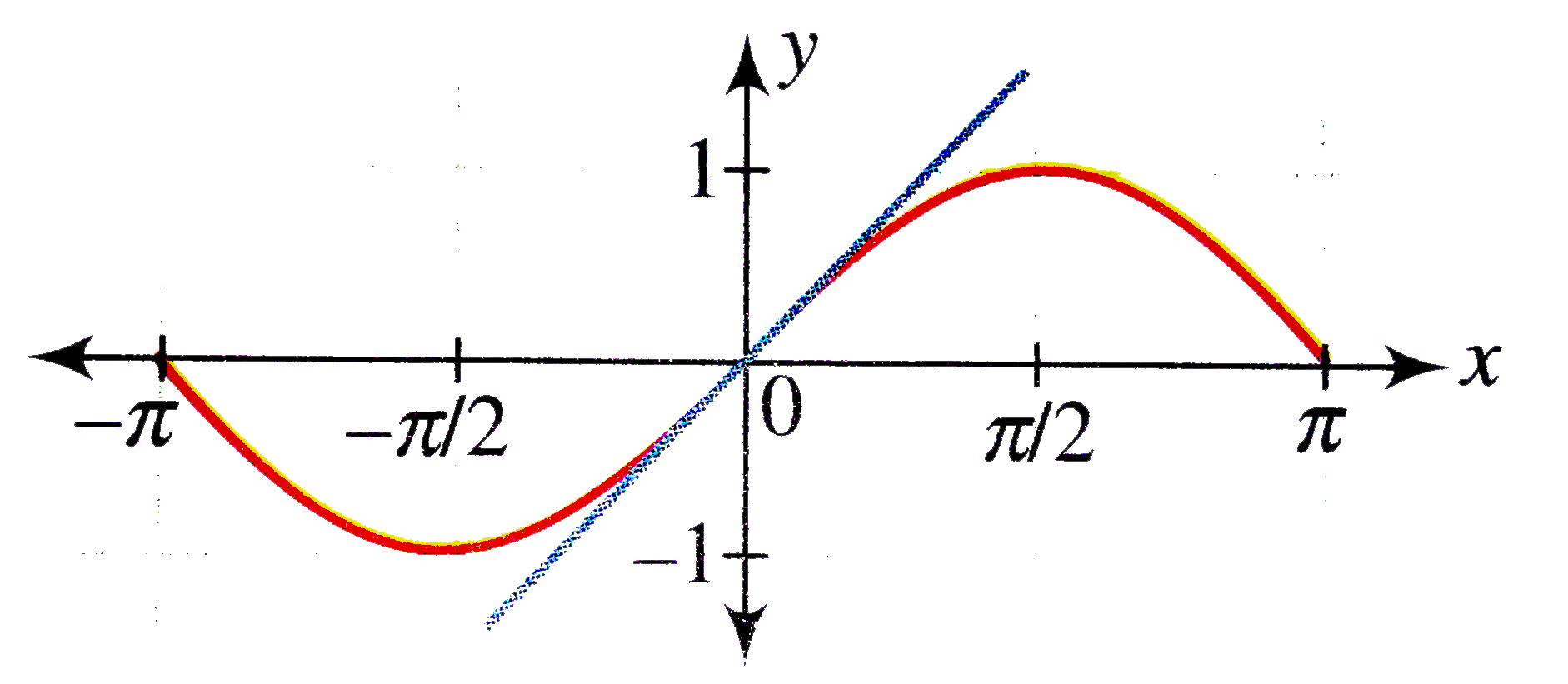
From the graph, when $x \to 0^{+}$ , as the graph of y = x is above the graph of y = sin x,
$sin x < x \Rightarrow \frac{sin x}{x} < 1 \Rightarrow [lim x \to 0^{+} \frac{sin x}{x}] = 0$
When $x \to 0^{-}$ , as the graph of y = x is below the graph of y = sin x,
$sin x > x \Rightarrow \frac{sin x}{x} < 1$ (as x is negative) $\Rightarrow [lim x \to 0^{-} \frac{sin x}{x}] = 0$
Thus, $[lim x \to 0 \frac{sin x}{x}] = 0$

Updated on:21/07/2023

$lim x \to 0 [(1 - e^{x}) \frac{sin x}{| x |}]$ is (where $[.]$ represents the greatest integer function )
A1
B2
C3
Dnone of these
The value of $lim x \to 0 [\frac{x}{sin x}]$ , where $[.]$ represents the greatest integer function,is
A1
B0
C-1
Dnone of these
The value of $lim x \to 0 \frac{sin x}{3} [\frac{5}{x}]$ is equal to
[where [.] represent the greatest integer function)
A $\frac{1}{3}$
B $0$
C $\frac{5}{3}$
D $1$