Prove that $[lim x \to 0 \frac{sin x}{x}] = 0,$ where $[.]$ represents the greatest integer function.

Video Solution

Text Solution

Verified by Experts

See the graphs of y=x and $sin x$ in the following figure.

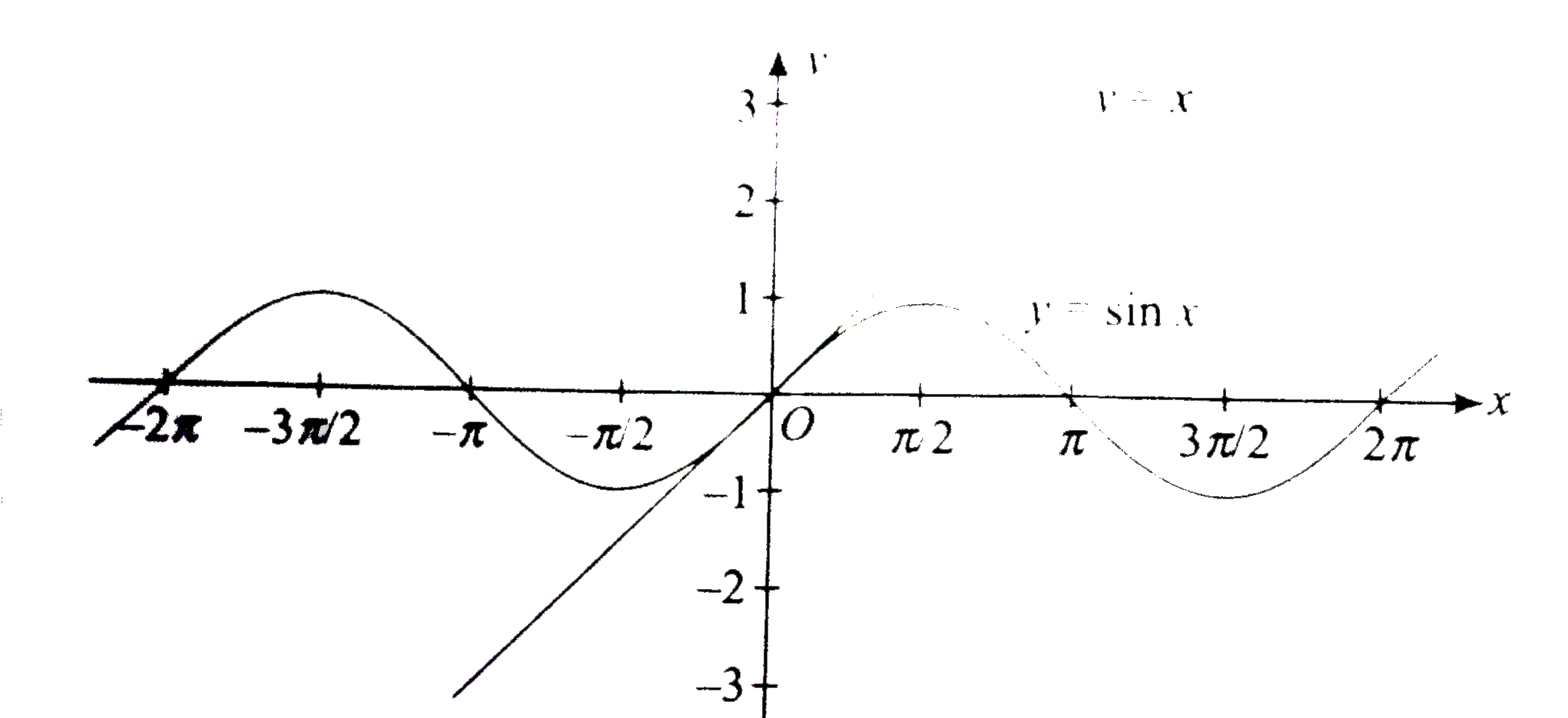
From the figure when $x \to 0^{+}$ ,graph of y=x is above the graph of $y = sin x$
i.e., $sin x < x or \frac{sin x}{x} < 1$
$\Rightarrow lim x \to 0^{+} \frac{sin x}{x} = 1^{1 -}$
$\Rightarrow [lim x \to 0^{+} \frac{sin x}{x}] = 0$
When $x \to 0^{-}$ , graph of y=x is below the graph of $y = sin x$
i.e., $sin x < x or \frac{sin x}{x} < 1$ (as x is negative)
$\Rightarrow lim x \to 0^{-} \frac{sin x}{x} = 1^{-}$
$\Rightarrow [lim x \to 0^{-} \frac{sin x}{x}] = 0$
Thus, $[lim x \to 0^{-} \frac{sin x}{x}] = 0$

Updated on:21/07/2023