Two identical balls AandB each of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is constrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horizontal plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radians with respect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the ball A when A and B are at the two ends of the diameter PQ.

The correct Answer is:(i)f=12π√4×010.1=1πHz,(ii)V=0.0628
(iii)3.9×10−4J
Given - Mass of each block A and B,m=0.1kg
Radius of circle, R=0.06m
Natural legth of spring l0=πR=0.06π (Half circle) and spring constant, k=0.1N/m
In the stretched position elongation in each spring
x=Rθ,
Let us draw FBD of A
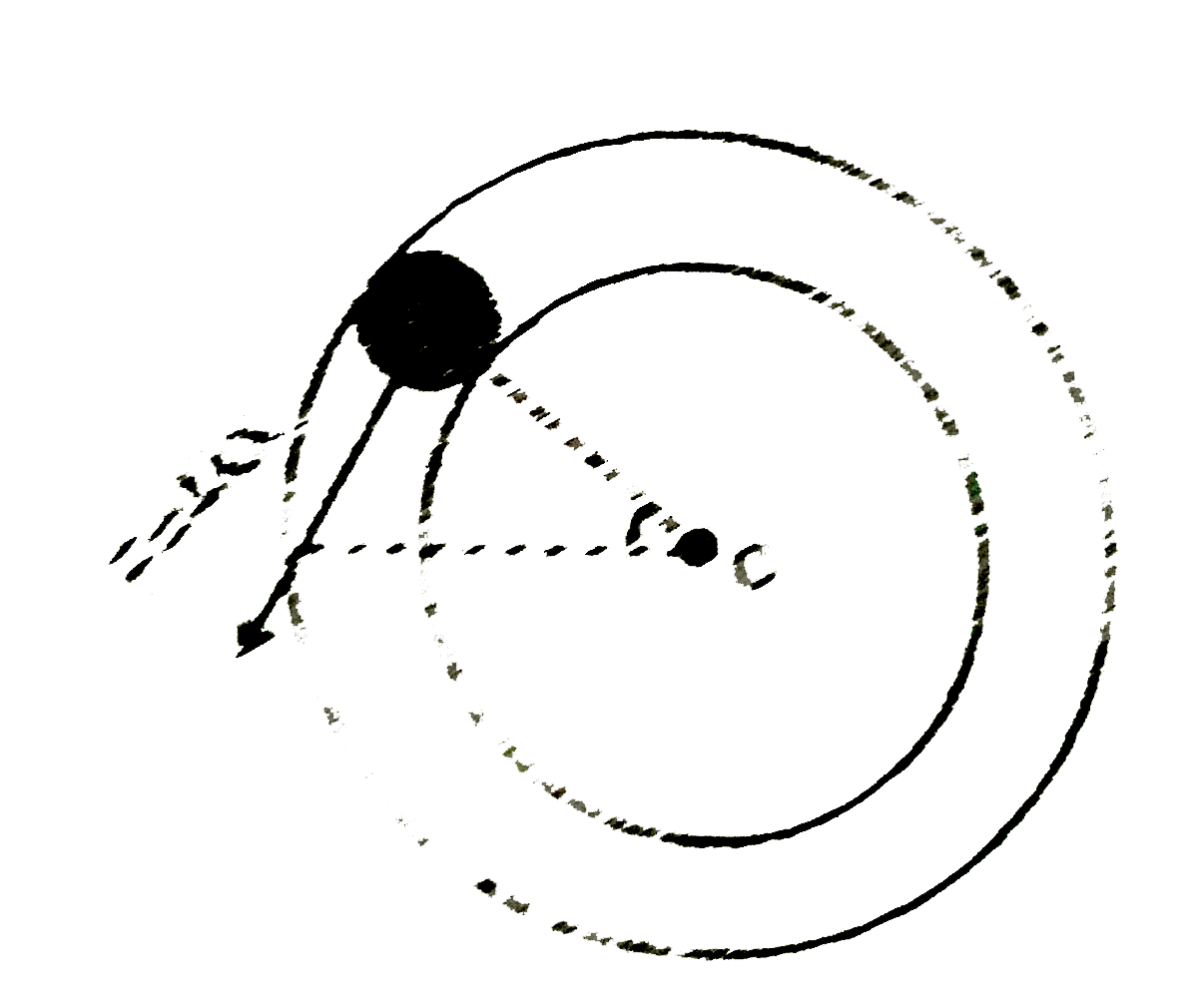
Spring in lower side is stretched by 2x and on upper side compressed by 2x. Therefore, each spring will exert a force 2kx on each ball.
Hence, a restoring force, F=4kx Will act on A in the direction shown in figure.
Restoring torq1ue of this force about again
τ=−F,R=−(4kx)R=−(4kRθ)R
or τ=−4kR2.θ.....(1)
Since, τ∝−θ, each ball executes angular SHM about origin O.
Eq. (1) can be rewritten as
lα=−4kR2θ
or (mR2)α=−4kR2θ
or α=−(4km)θ
∴ Frequency of oscillation, f=12π√∣∣∣accelerationdisplacement∣∣∣=12π√∣∣∣αθ∣∣∣
f=12π√4×0.10.1=1πHz.
Alternate :
f=12π√k'μ
where k'=2k,μ=m1m2m1+m2=m2
f=12π√4km=12π√4×0.10.1=1πHz
(ii) In stretched position, potential energy of the system is
PE=2{12k}{2x}2=4kx2,(x=Rπ6)
and in mean position, both the blocks have kinetic energy only. Hence,
KE=2{12mv2max
From energy conservation
PE=KE
∴4kx2=mv2max
∴vmax=2x√km=2Rθ√km
Substituting the values
vmax=2(0.06)(π/6)√0.10.1=0.02π1
or vmax=0.0628m/s
(iii) Total energy of the system, E=PE in stretched position
or =KE at mean position
E=2(12mv2max)=(0.1)(0.0628)2J or E=3.9×10−4J
Topper's Solved these Questions
Similar Questions
Two identical balls AandB eavh of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced bu an angle θ=π/6 dadius withrespect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.
 View Solution
View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
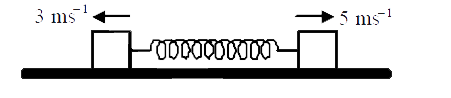
Choose the correct statement -View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk - Question 2 - Select One
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
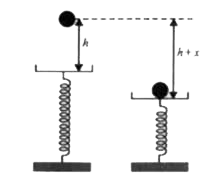 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x) - Question 3 - Select One
Two identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
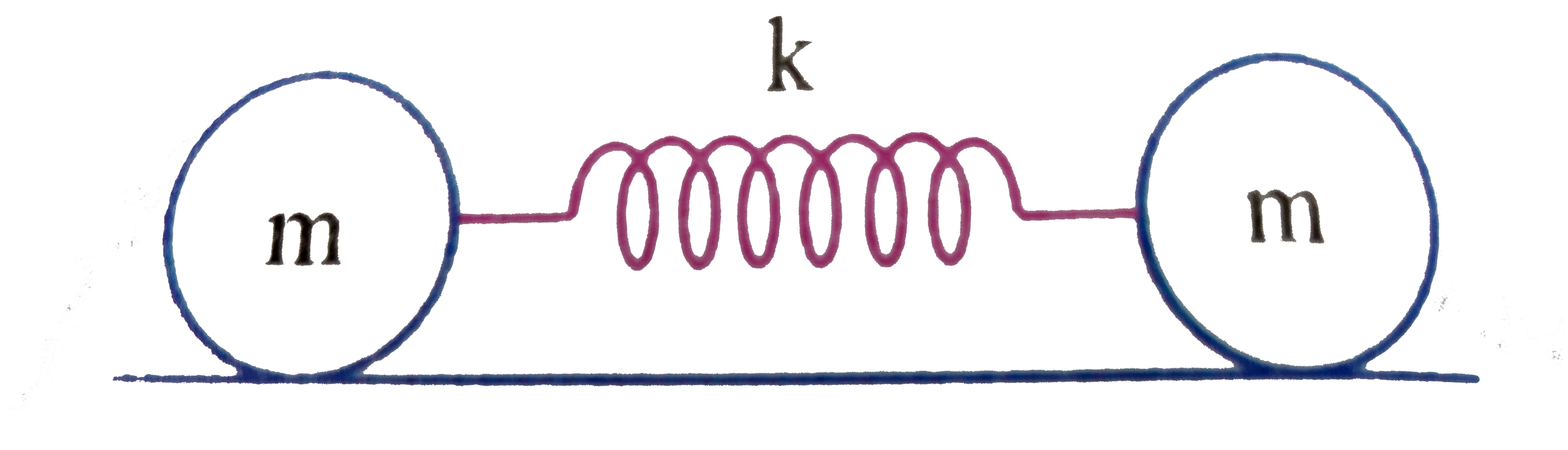 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10s
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is
 View Solution
View SolutionTwo masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B wil be :-
 View Solution
View SolutionTwo identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is
 View Solution
View SolutionTwo bodies A and B each of mass M are fixed together by a massless spring A force F acts on the mass B as shown in fig At the instant shown the mass A has acceleration a. What is the acceleration of mass B?
 View Solution
View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length
 View Solution
View Solution

