Question

The period of oscillation of a simple pendulum of length $L$ suspended from the roof of a vehicle which moves without frication down on inclined plane of inclination $lpha={60}^{\circ }$ is given by $\pi \sqrt{\frac{XL}{g}}$ then find $X$.

Answer

8

Explanation

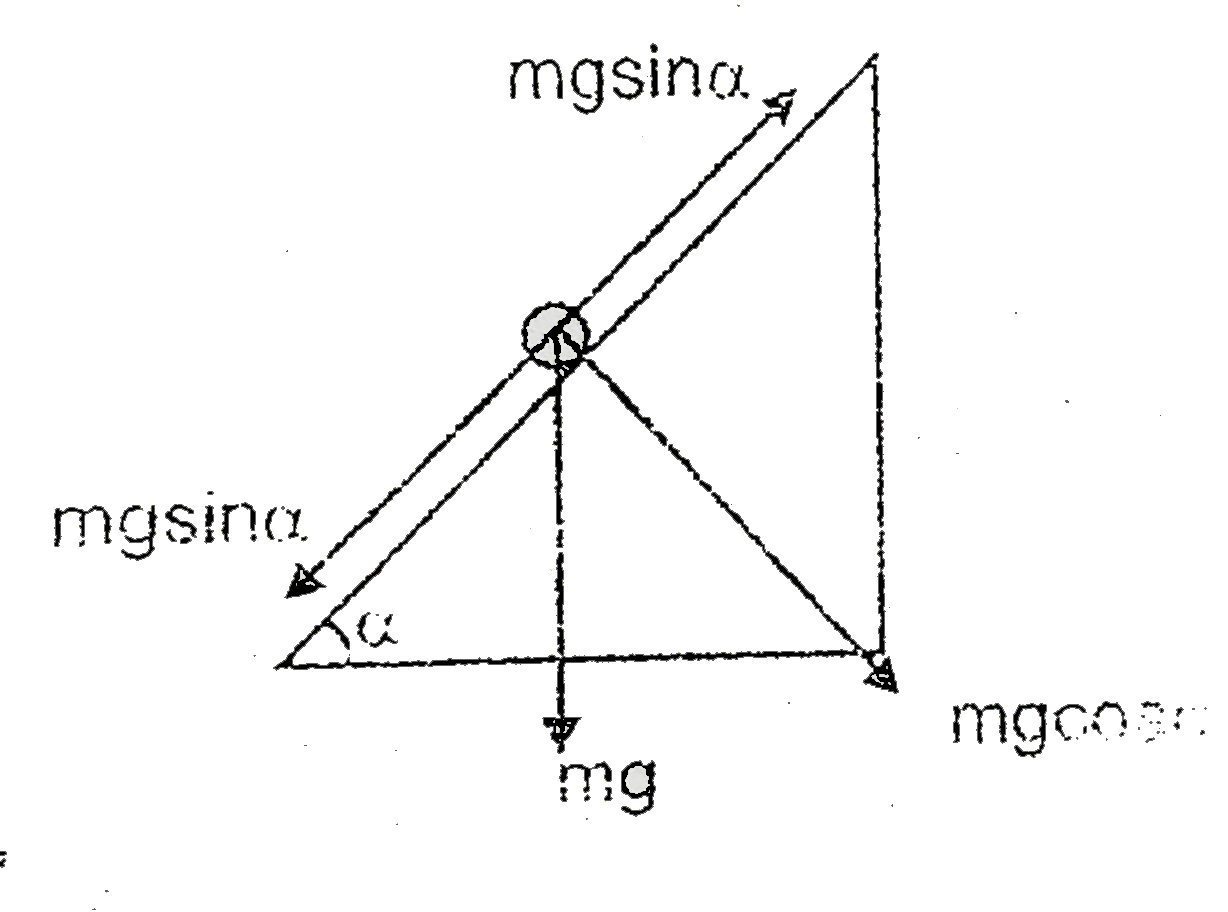
Free body diagram of bob of the pendulum with respect to the acclerating frame of refrenence is as follows:
`:.` Net tension in the string is `T = mg cos alpha`
So, `g_(eff) = (T)/(m) = (mgcosalpha)/(m) = g cos alpha`
`T = 2pisqrt((L)/(g_(eff)))` or `T = 2pisqrt((T)/(gcosalpha))`

Alternative :
Whenever point of suspension acclerating
Take `T = 2pisqrt((L)/(g_(eff)))` Where `overset(vec)(g_(eff)) = overset(vec)(g) - overset(vec)(a)`
`overset(vec)(a) =` Acceleration of point of suspension.
In this quesion `overset(vec)(a) = g sin alpha` (down the plane)
`:. |overset(vec)(g)-overset(vec)(a)| = g_(eff) = sqrt(g^(2) + (gsinalpha)^(2) + 2(g)(gsinalpha)cos(90^(@) + alpha)) = g cos alpha`
`:. T = 2pi sqrt((T)/(gcosalpha)) (alpha = 60^(@))`
`T = 2pisqrt((2L)/(g)) :. x = 2`
`T = t_(0) = 2pi sqrt(((l)/(g))) ....(1)`
`l`, being the length of simple pendulum
in water, effective weight of bob
`w' =` weight of bob in air `-` unthrust
`rArr rhoVg_(eff) = mg - m'g`
`= rhoVg - rho'Vg = (rho - rho')Vg`
where `rho =` density of bob,
`rho' density of water
`:. g_(eff) = ((rho - rho')/(rho))g = (1-(rho')/(rho))g`
`:. t = 2pi sqrt((l)/([(1-(rho')/(rho))g])) = sqrt[((1)/(1-(1000)/(4//3)xx1000))]=2`
`rArr t = 2 t_(0) , (t)/(t_(0)) = 2`
`:. N = 2`