A solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
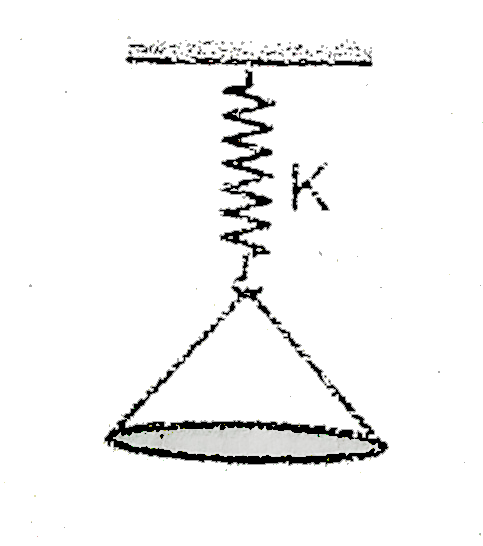
mgK
mgk(1+2HKmg)1/2
mgK+(2HKmg)1/2
mgK[1+(1+2HKmg)1/2]
The correct Answer is:B
Step by step video, text & image solution for A solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III
12 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
37 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
A load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is
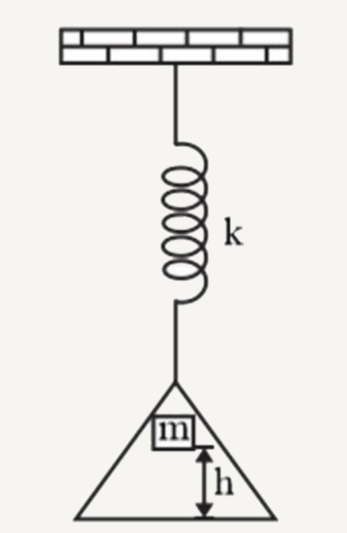
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View Solution
Knowledge Check
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4A solid sphere rolls without slipping and presses a spring of spring constant k as shown in figure. Then, the compression in the spring will be
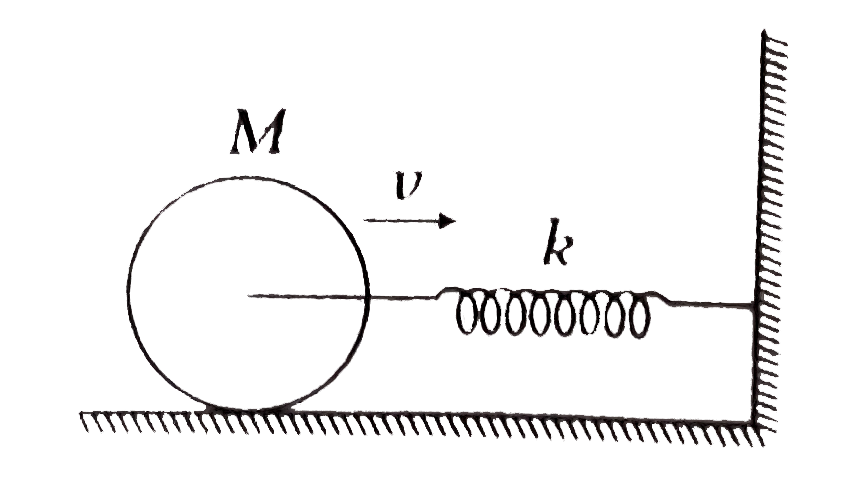 Av√2M3kBv√2M5kCv√5k7MDv√7M5k
Av√2M3kBv√2M5kCv√5k7MDv√7M5kA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is
 AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
AmgkBmgk√1+2hkmgCmgk+mgk√1+2hkmgDNone of these
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

View SolutionA body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring , as shown in the figure . If the spring constant is k , mass of the not bounce , relative to the pan , then the amplitude of vibration is

View SolutionA load of mass m falls from a height h on to the scale pan hung from a spring as shown in the adjoining figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is

View Solution
