A street car moves rectilinearly from station A (here car stops) to the next station B (here also car stops) with an acceleration varying according to the law f=a−bx, where a and b are positive constants and x is the distance from station A. If the maximum distance between the two stations is x=Nab then find N.
The correct Answer is:2
f=a−bx
For maximum velocity, acceleration should be zero.
i.e. a−bx=0⇒x=ab
∴ At x=ab, the particle has its maximum velocity
f=vdvdx=a−bx⇒v22=ax−bx22+c
At x=0,v=0⇒c=0
Substituting : x=ab, gives
vmax=a√b
Also, the velocity of the car should become zero at station B.
i.e. ax−bx22=0⇒x=0,x=(2ab)
∴ Distance between the two stations is (2a)(b)
∴N=2
Alternate : f=a−bx means particle will do SHM.
At mean position , f=0
⇒x=ab⇒ 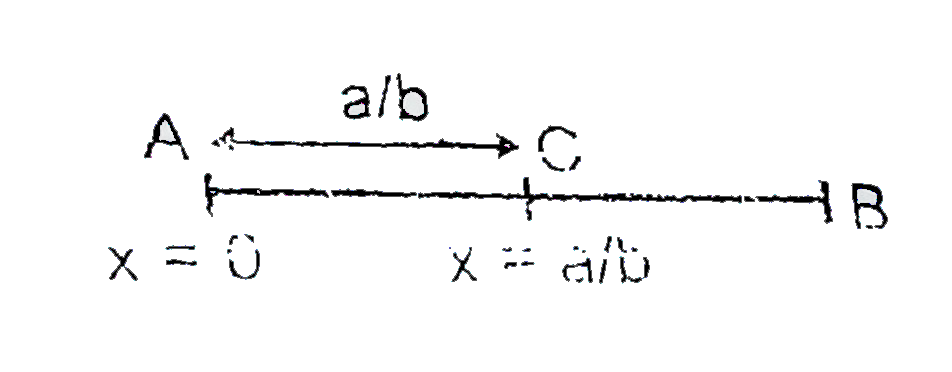
In the figure shown, 'C' is the mean positions and A & B are extreme positions
∴xmax=2ab
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III
12 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
37 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
A car starts moving from rest on a horizontal ground such that the position vector of car with respect to its starting point is given as →r=btˆi−ct2ˆj, where a and b are position constants, direction (x and y axes) intersect at the starting point of car (origin). Find:
(a) The equation of the trajectory of car y=f(x).
(b) The angle between direction of velocity and acceleration of car as a function of time θ=f(t).
(c) Average velocity of car over first t seconds of motion
View SolutionWhile travelling from one station to another , a car travels 75km north , 60km north - east and 20km east. The minimum distance between the two station is
View Solution
Knowledge Check
A street car moves rectilinearly from station A to the next station B (from rest to rest) with an acceleration varying according to the law f=a−bx, where a and b are constants and x is the distance from station A. The distance between the two stations and the maximum velocity are
Ax=2ab,vmax=a√bBx=a2b,vmax=abCx=a2b,vmax=b√aDx=ab,vmax=√abA street car moves rectilinearly from station A to the next station B with an acceleration varying according to the law f=a−bx, where a and b are constants and x is the distance from station A. The distance between the two stations & the maximum velocity are :
Ax=2ab,vmax=a√bBx=b2a,vmax=abCx=a2b,vmax=b√aDx=ab,vmax=√abThe speed v of a car moving on a straight road changes according to equation, v2=1+bx, where aandb are positive constants. Then the magnitude of acceleration in the course of such motion : (x is the distance travelled).
AincreasesBdecreasesCstay constantDfirst decreases and then increases
A train starts from station A and reaches B 15 minutes late when it moves with 40 km/hr and 24 minutes late when it goes 30 km/hr. The distance between the two stations is
View SolutionA train starts from station A and reaches B 15 minutes late when it moves with 40 km/hr and 24 minutes late when it goes 30 km/hr. The distance between the two stations is
View SolutionA train starts from rest and moves with uniform acceleration α for some time and acquires a velocity v it then moves with constant velocity for some time and then decelerates at rate β and finally comes to rest at the next station. If L is distance between two stations then total time of travel is
View SolutionTwo stations A and B, 100 km far away to each other. Two trains starts at the same time from station A and station B. The train starts from station A is running with the speed of 50 km/h to station B. The train starts from station
B is running with the speed of 75 km/h to station A. At what distance both the trains meet with each other from station A?
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
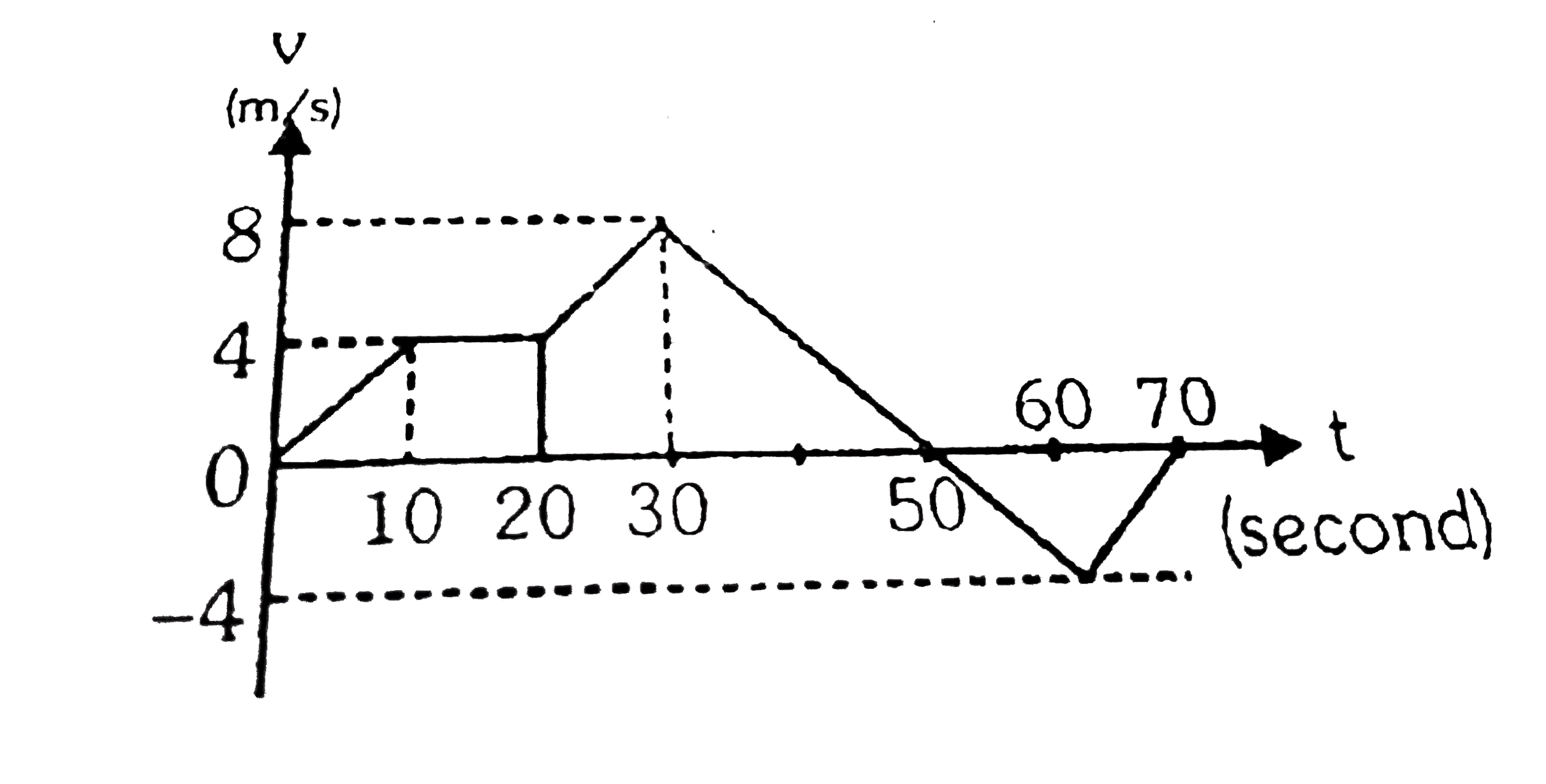
The maximum displacement from the starting position will be :-
View Solution
