A train starts from rest and moves with uniform acceleration for some time and acquires a velocity it then moves with constant velocity for some time and then decelerates at rate and finally comes to rest at the next station. If L is distance between two stations then total time of travel is
The correct Answer is:A
To solve the problem step by step, we will break down the journey of the train into three parts: acceleration, constant velocity, and deceleration.
Step 1: Calculate Time for Acceleration (T1)
The train starts from rest and accelerates uniformly with acceleration α until it reaches a velocity v.
Using the equation of motion:
v=u+at
where u=0 (initial velocity), a=α, and v is the final velocity.
Rearranging gives:
t1=v−0α=vα
Step 2: Calculate Distance Covered During Acceleration (s1)
Using the equation of motion:
s=ut+12at2
Substituting u=0, we get:
s1=0+12αt21
Substituting t1=vα:
s1=12α(vα)2=v22α
Step 3: Calculate Time for Constant Velocity (T2)
During the constant velocity phase, the distance covered is s2. The total distance L is given, and we need to find s2:
s2=L−s1−s3
where s3 is the distance covered during deceleration.
Step 4: Calculate Time for Deceleration (T3)
The train decelerates at a rate β until it comes to rest. Using the equation:
0=v−βt3
Rearranging gives:
t3=vβ
Step 5: Calculate Distance Covered During Deceleration (s3)
Using the equation of motion:
0=v2−2βs3
Rearranging gives:
s3=v22β
Step 6: Substitute s1 and s3 into s2
Now we can find s2:
s2=L−s1−s3=L−v22α−v22β
Combining the terms gives:
s2=L−v22(1α+1β)
Step 7: Calculate Time for Constant Velocity (T2)
Now we can find T2:
t2=s2v=L−v22(1α+1β)v
Step 8: Total Time of Travel
The total time T is the sum of all three times:
T=t1+t2+t3
Substituting the values we found:
T=vα+(Lv−v2(1α+1β))+vβ
Simplifying gives:
T=Lv+v2(1α+1β)
Final Answer
Thus, the total time of travel is:
T=Lv+v2(1α+1β)
The train starts from rest and accelerates uniformly with acceleration α until it reaches a velocity v.
v=u+at
where u=0 (initial velocity), a=α, and v is the final velocity.
t1=v−0α=vα
Using the equation of motion:
s=ut+12at2
Substituting u=0, we get:
s1=0+12αt21
Substituting t1=vα:
s1=12α(vα)2=v22α
During the constant velocity phase, the distance covered is s2. The total distance L is given, and we need to find s2:
s2=L−s1−s3
where s3 is the distance covered during deceleration.
The train decelerates at a rate β until it comes to rest. Using the equation:
0=v−βt3
Rearranging gives:
t3=vβ
Using the equation of motion:
0=v2−2βs3
Rearranging gives:
s3=v22β
Now we can find s2:
s2=L−s1−s3=L−v22α−v22β
Combining the terms gives:
s2=L−v22(1α+1β)
Now we can find T2:
t2=s2v=L−v22(1α+1β)v
The total time T is the sum of all three times:
T=t1+t2+t3
Substituting the values we found:
T=vα+(Lv−v2(1α+1β))+vβ
Simplifying gives:
T=Lv+v2(1α+1β)
Thus, the total time of travel is:
T=Lv+v2(1α+1β)
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Single Type Question
Explore 23 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:More than One Option Question
Explore 7 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 C.W
Explore 25 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
A train starting from rest moves with a uniform acceleration of 0.2m/s2 for 5 minutes . Calculate the speed acquired and the distance travelled in this time.
View SolutionA car moves in a straight line, the car accelerates from rest with a constant acceleraation α on a straight foad. After gaining a velocity v, the car moves with that velocity for somerime. Then car decelerates with a retardation β, If the total distance covered by the car is equal to s find the total time of its motion.
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A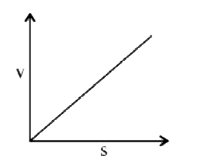 B
B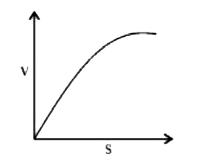 C
C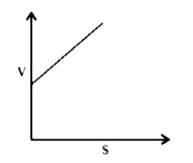 D
D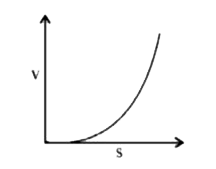
A car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
AaT4B3aT2CaT2DaTA train moves from rest with acceleration α and in time t1 covers a distance x. It then decelerates rest at constant retardation β for distance y in time t2. Then
Axy=βαBβα=t1t2Cx=yDxy=βt1αt2
A train starting from rest moves with a uniform acceleration of 0.2m/s2 for 5 minutes . Calculate the speed acquired and the distance travelled in this time.
View SolutionA car starts from rest and moves with uniform acceleration for time t then it moves with uniform speed of 60 km/h for time 3t and comes to rest. Find the average speed of car in its total journey.
View SolutionA car starts from rest and moves with uniform acceleration a, At the same instant from the same point a bike crosses with a uniform velocity u. When and there will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View SolutionA train goes from rest to rest between two stations with uniform acceleration and retardation. Find the rato of maximum velocity of the average velocity.
View SolutionA car, starting from rest, accelerates at the rate f through a distance s, then continues at constant speed for time t and then decelerates at the rate f/ 2 to come to rest. If the total distance travelled is 15 s, then
View Solution