The friction of the air causes a vertical retardation equal to 10% of the acceleration due to gravity. Take g=10m/s2 the maximum height and time to reach the maximum height will be decreased by
9%,9%
11%,11%
9%,10%
11%,9%
The correct Answer is:A
To solve the problem, we need to determine how the maximum height and the time to reach that maximum height are affected by the air resistance, which causes a vertical retardation equal to 10% of the acceleration due to gravity.
1. Understanding the Given Values:
- The acceleration due to gravity g=10m/s2.
- The air resistance causes a vertical retardation of 10% of g.
- Therefore, the effective acceleration due to gravity when considering air resistance is:
geffective=g+retardation=g+0.1g=1.1g=1.1×10=11m/s2
2. Finding the Maximum Height Without Air Resistance:
- The formula for the maximum height H reached by a projectile when air resistance is neglected is given by:
H=u22g
- Substituting the value of g:
H=u22×10=u220
3. Finding the Maximum Height With Air Resistance:
- The new maximum height H′ when considering air resistance is:
H′=u22geffective=u22×11=u222
4. Calculating the Decrease in Height:
- The decrease in height ΔH can be calculated as:
ΔH=H−H′=u220−u222
- To find a common denominator:
ΔH=11u2−10u2220=u2220
- The percentage decrease in height is given by:
ΔHH×100=u2220u220×100=20220×100=10011≈9.09%
5. Finding the Time to Reach Maximum Height Without Air Resistance:
- The time t to reach maximum height without air resistance is given by:
t=ug=u10
6. Finding the Time to Reach Maximum Height With Air Resistance:
- The new time t′ to reach maximum height with air resistance is:
t′=ugeffective=u11
7. Calculating the Decrease in Time:
- The decrease in time Δt is:
Δt=t−t′=u10−u11
- Finding a common denominator:
Δt=11u−10u110=u110
- The percentage decrease in time is given by:
Δtt×100=u110u10×100=10110×100=10011≈9.09%
Final Result:
Both the maximum height and the time to reach the maximum height will be decreased by approximately 9%.
- The acceleration due to gravity g=10m/s2.
- The air resistance causes a vertical retardation of 10% of g.
- Therefore, the effective acceleration due to gravity when considering air resistance is:
geffective=g+retardation=g+0.1g=1.1g=1.1×10=11m/s2
- The formula for the maximum height H reached by a projectile when air resistance is neglected is given by:
H=u22g
- Substituting the value of g:
H=u22×10=u220
- The new maximum height H′ when considering air resistance is:
H′=u22geffective=u22×11=u222
- The decrease in height ΔH can be calculated as:
ΔH=H−H′=u220−u222
- To find a common denominator:
ΔH=11u2−10u2220=u2220
- The percentage decrease in height is given by:
ΔHH×100=u2220u220×100=20220×100=10011≈9.09%
- The time t to reach maximum height without air resistance is given by:
t=ug=u10
- The new time t′ to reach maximum height with air resistance is:
t′=ugeffective=u11
- The decrease in time Δt is:
Δt=t−t′=u10−u11
- Finding a common denominator:
Δt=11u−10u110=u110
- The percentage decrease in time is given by:
Δtt×100=u110u10×100=10110×100=10011≈9.09%
Both the maximum height and the time to reach the maximum height will be decreased by approximately 9%.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Single Type Question
Explore 23 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:More than One Option Question
Explore 7 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 C.W
Explore 25 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
Knowledge Check
The friction of the air causes a vertical retardation equal to 10% of the acceleration due to gravity, take (g=10ms−2). The maximum height will be decreased by:
A8%B9%C10%D11%In the previous problem, the time taken to reach the maximum height will be decreased by:
A19%B5%C10%Dnone of theseAcceleration the due to gravity become [g2] at a height equal to
A4RBR4C2RDR2
If acceleration due to gravity is 10m/s2, what will be the potential energy of a body of mass 1 kg kept at a height of 5 m?
View SolutionQuestion Stimulus
A stone is thrown vertically upwards with an initial velocity of 30ms−1. Acceleration due to gravity g=10ms−2. The maximum height reached by the stone is
View SolutionIf retardation produced by air resistances to projectile is one-tenth of acceleration due to gravity, the time to reach maximum height approximately-
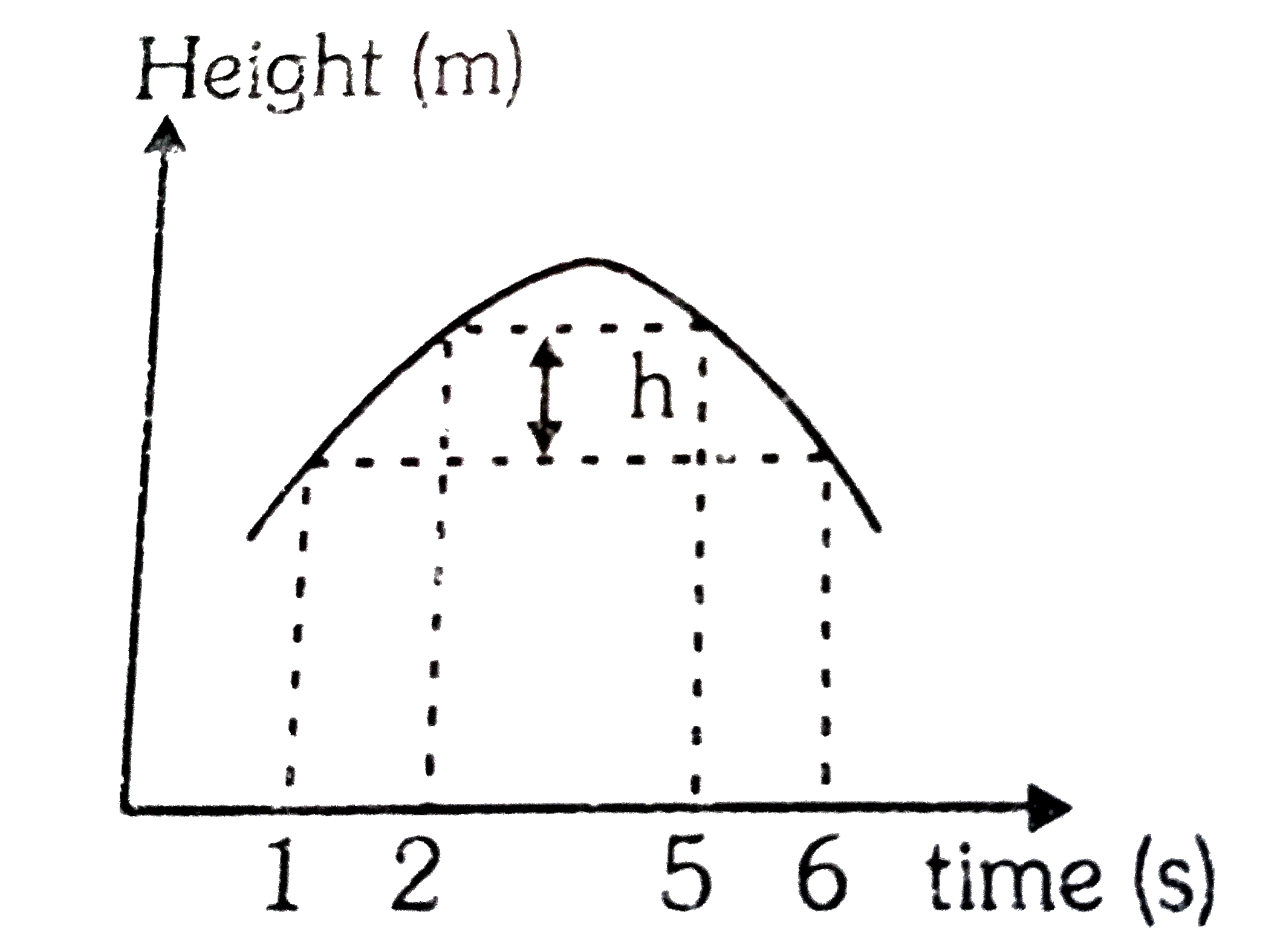
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
View SolutionIf radius of earth decreases by 10%, then acceleration due to gravity (Density of earth remain constant)
View Solution

