A rod of mass $M$ and length $L$ is hinged at its one end and carries a particle of mass $m$ at its lower end. A spring of force constant $k_{1}$ is installed at distance a from the hinge and another of force constant $k_{2}$ at $B$ distance $b$ as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :

A

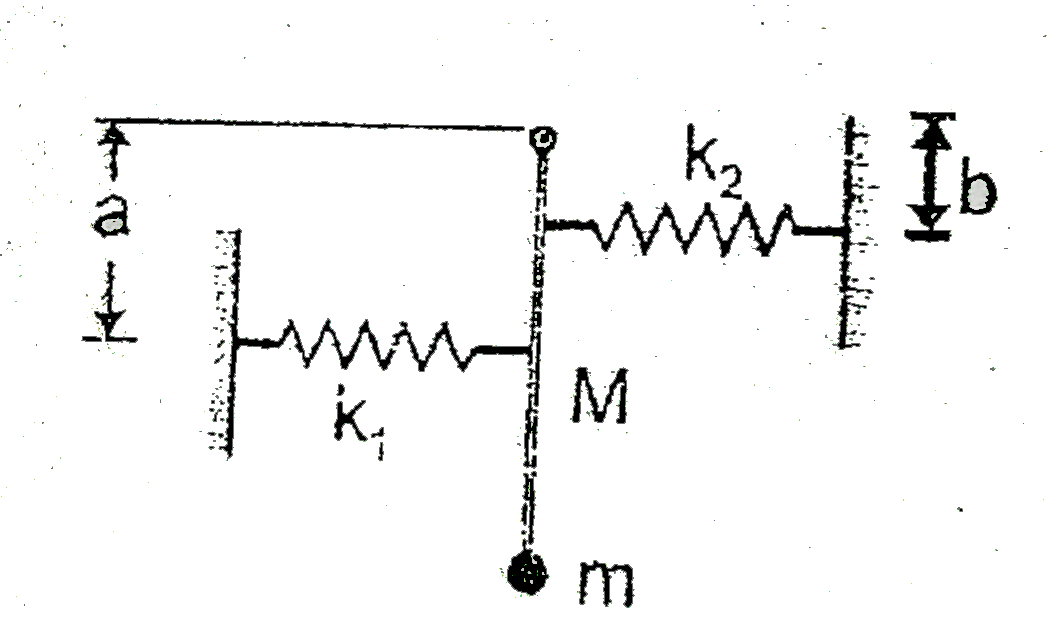
$\frac{1}{2 π} \sqrt{\frac{k_{1} a^{2} + k_{2} b^{2}}{L^{2} (m + \frac{M}{3})}}$

B

$\frac{1}{2 π} \sqrt{\frac{k_{2} + k_{1}}{M + m}}$

C

$\frac{1}{2 π} \sqrt{\frac{k_{2} + k_{1} \frac{a_{2}}{b^{2}}}{4 \frac{M}{3} + m}}$

D

$\frac{1}{2 π} \sqrt{\frac{k_{1} + \frac{k_{2} b_{2}}{a^{2}}}{\frac{4}{3} m + M}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

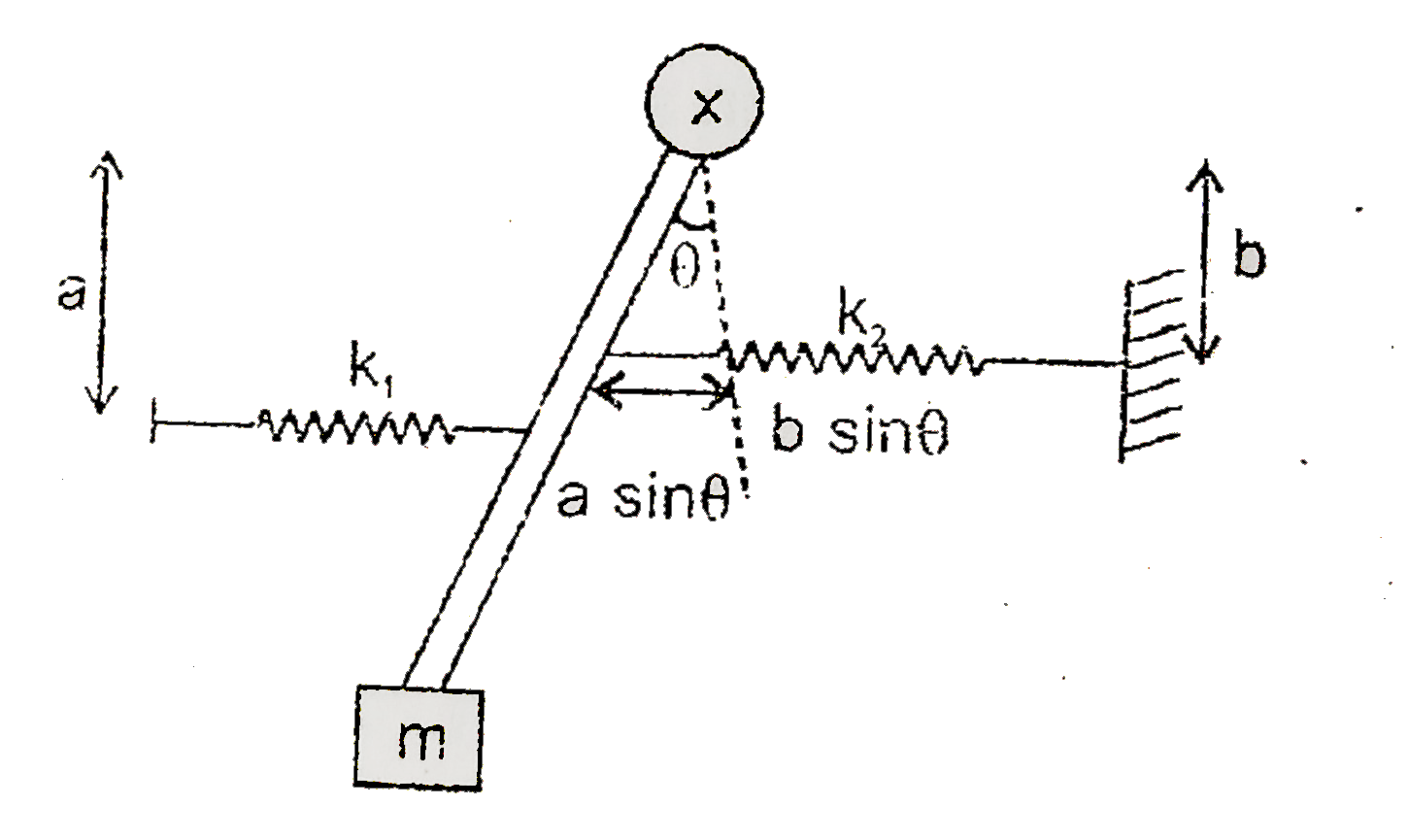
For small angular displacement $(θ)$
Net torque on body $= I α$
$= (k_{1} a sin θ) a + (k_{2} b sin θ) b = (m L^{2} + \frac{M L^{2}}{3}) α$
For small $θ \Rightarrow a = \frac{k_{1} a^{2} + k_{2} b^{2}}{m L^{2} + \frac{M L^{2}}{3}} θ \Rightarrow$ frequency $= \frac{1}{2 π} \sqrt{\frac{k_{1} a^{2} + k_{2} b^{2}}{L^{2} (m + M / 3)}}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A thin uniform rod mass $M$ and length $L$ is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance $L / 3$ from the hinge point, when the rod become vertical will
A $22 M g / 27$
B $11 M g / 13$
C $6 M g / 11$
D $2 M g$
Question 2 - Select One
A rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-

A $\frac{3 M g}{K}$
B $\frac{M g}{K}$
C $\frac{2 M g}{K}$
D $\frac{4 M g}{K}$
Question 3 - Select One
A rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal

A $\frac{m g}{4}$
B $\frac{3 m g}{2} cos θ$
C $\frac{m g}{4} \sqrt{9 {cos}^{2} θ + \frac{1}{4}}$
D $\frac{m g}{2} \sqrt{9 {cos}^{2} θ + \frac{1}{4}}$

RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 2, PART - I

Home
Ask Doubt
Profile