According to a scientists, he applied a force F=−cx1/3 on a particle and the particle is performing SHM. No other force acted on the particle. He refuses to tell whether c is a constant or not. Assume that he had worked only with positive x then :
as x increases c also increases
as x increases c also decreases
as x increases c remain constant
the motion cannot be SHM
The correct Answer is:A
To solve the problem, we need to analyze the force applied to the particle and its implications for simple harmonic motion (SHM). The force given is F=−cx1/3.
1. Understanding the Force:
The force acting on the particle is given by F=−cx1/3. This indicates that the force is dependent on the displacement x raised to the power of 13.
2. Identifying the Form of SHM:
In simple harmonic motion, the restoring force is typically proportional to the negative of the displacement, which can be expressed as F=−kx, where k is a constant. For SHM to occur, the force must be linear in x.
3. Comparing with SHM Condition:
The given force F=−cx1/3 does not have a linear relationship with x (since x1/3 is not linear). Therefore, this force does not satisfy the condition for SHM.
4. Conclusion about the Nature of Motion:
Since the force does not lead to a linear restoring force, the particle cannot be undergoing simple harmonic motion. Thus, the correct conclusion is that the motion cannot be simple harmonic motion.
5. Evaluating the Options:
Based on the analysis, we can evaluate the options provided:
- Option 1: As x increases, c also increases. (Not necessarily true)
- Option 2: As x increases, c also decreases. (Not necessarily true)
- Option 3: As x increases, c remains constant. (This is the most plausible if c is considered constant)
- Option 4: The motion cannot be simple harmonic motion. (This is correct)
Thus, the correct answer is that the motion cannot be simple harmonic motion.
Final Answer:
The correct option is: The motion cannot be simple harmonic motion.
The force acting on the particle is given by F=−cx1/3. This indicates that the force is dependent on the displacement x raised to the power of 13.
In simple harmonic motion, the restoring force is typically proportional to the negative of the displacement, which can be expressed as F=−kx, where k is a constant. For SHM to occur, the force must be linear in x.
The given force F=−cx1/3 does not have a linear relationship with x (since x1/3 is not linear). Therefore, this force does not satisfy the condition for SHM.
Since the force does not lead to a linear restoring force, the particle cannot be undergoing simple harmonic motion. Thus, the correct conclusion is that the motion cannot be simple harmonic motion.
Based on the analysis, we can evaluate the options provided:
- Option 1: As x increases, c also increases. (Not necessarily true)
- Option 2: As x increases, c also decreases. (Not necessarily true)
- Option 3: As x increases, c remains constant. (This is the most plausible if c is considered constant)
- Option 4: The motion cannot be simple harmonic motion. (This is correct)
The correct option is: The motion cannot be simple harmonic motion.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - I
Explore 26 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - I
Explore 25 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
A student says that he had applied a force F=−k√x on a particle and the particle moved in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle
View SolutionA time dependent force F=3t^(2)+6t acts on a particle of mass 18kg .If particle starts from rest the work done by the force during the first 3 second will be :
View Solution
Knowledge Check
A student says that he had applied a force F=−k√x on a particle and the particle performs in simple harmonic motion. He refuses to tell whether k is a constant or not. Assume that he has worked only with positive x and no other force acted on the particle.
AAs X increases k increasesBAs X increases K decreasesCAs X increases k remains constantDThe motion cannot be simple harmonicA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
A9JB18JC4.5JD22JA position dependent force F ia acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from 0 to 5 m is
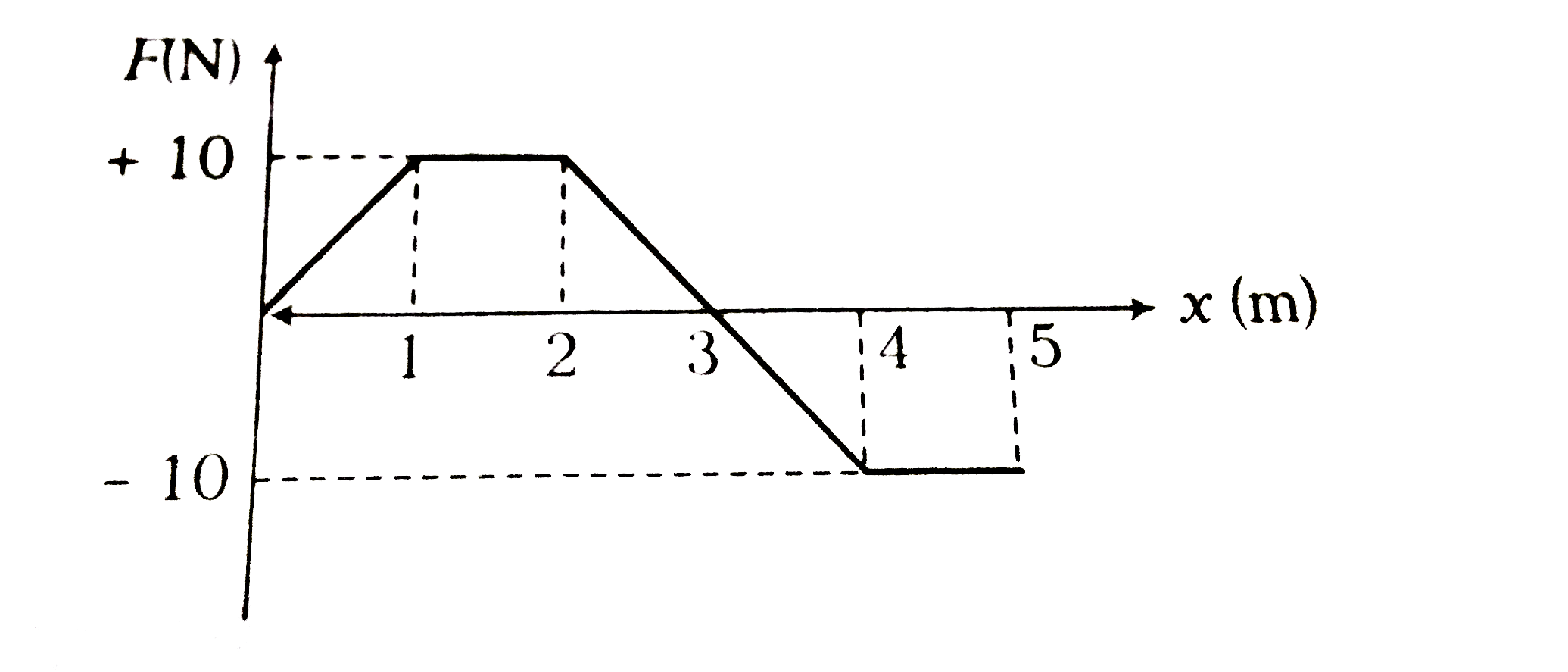 A35 JB25 JC15 JD5 J
A35 JB25 JC15 JD5 J
The power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with displacement as x1K. Find the value of K.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA force F=20+10y acts on a particle in y-direction where F is in Newton and y in meter. Wrok done by this force to move the particle from y=0 to y=1m is:
View Solution