A force F=Kx2 acts on a particle at an angle of 60° with the x–axis. the work done in displacing the particle from x1 to x2 will be –
kx22
k2(x22−x21)
k6(x32−x31)
k3(x32−x31)
The correct Answer is:C
To solve the problem of calculating the work done by the force F=Kx2 acting at an angle of 60∘ with the x-axis while displacing the particle from x1 to x2, we can follow these steps:
Step 1: Identify the Components of the Force
The force F acts at an angle of 60∘ to the x-axis. The x-component of the force is given by:
Fx=Fcos(60∘)=Kx2⋅12=Kx22
Step 2: Write the Expression for Work Done
The work done dW by the force when the particle is displaced by an infinitesimal distance dx is given by:
dW=Fx⋅dx=Kx22⋅dx
Step 3: Integrate to Find Total Work Done
To find the total work done in displacing the particle from x1 to x2, we need to integrate dW:
W=∫x2x1dW=∫x2x1Kx22dx
Step 4: Perform the Integration
Now we can perform the integration:
W=K2∫x2x1x2dx
The integral of x2 is:
∫x2dx=x33
Thus, we have:
W=K2(x33)x2x1
Step 5: Substitute the Limits
Now substituting the limits x1 and x2:
W=K2(x323−x313)
This simplifies to:
W=K6(x32−x31)
Final Answer
Thus, the work done in displacing the particle from x1 to x2 is:
W=K6(x32−x31)
---
The force F acts at an angle of 60∘ to the x-axis. The x-component of the force is given by:
Fx=Fcos(60∘)=Kx2⋅12=Kx22
The work done dW by the force when the particle is displaced by an infinitesimal distance dx is given by:
dW=Fx⋅dx=Kx22⋅dx
To find the total work done in displacing the particle from x1 to x2, we need to integrate dW:
W=∫x2x1dW=∫x2x1Kx22dx
Now we can perform the integration:
W=K2∫x2x1x2dx
The integral of x2 is:
∫x2dx=x33
Thus, we have:
W=K2(x33)x2x1
Now substituting the limits x1 and x2:
W=K2(x323−x313)
This simplifies to:
W=K6(x32−x31)
Thus, the work done in displacing the particle from x1 to x2 is:
W=K6(x32−x31)
Topper's Solved these Questions
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-A
Explore 25 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 3 Section-B
Explore 22 Videos
- WORK, POWER & ENERGY Book:MOTIONChapter:WORK, POWER & ENERGY Exercise:Exercise - 1
Explore 42 Videos
- WAVESBook:MOTIONChapter:WAVESExercise:EXERCISE -4 (Level -II) (previous year JEE Advanced)
Explore 10 Videos
Similar Questions
A force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionIf force F=(2x+3x2)N is applied on a particle along x = axis, then find the work done by it during motion of particle from x = 0 to x = 2 m.
View Solution
Knowledge Check
A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−akA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
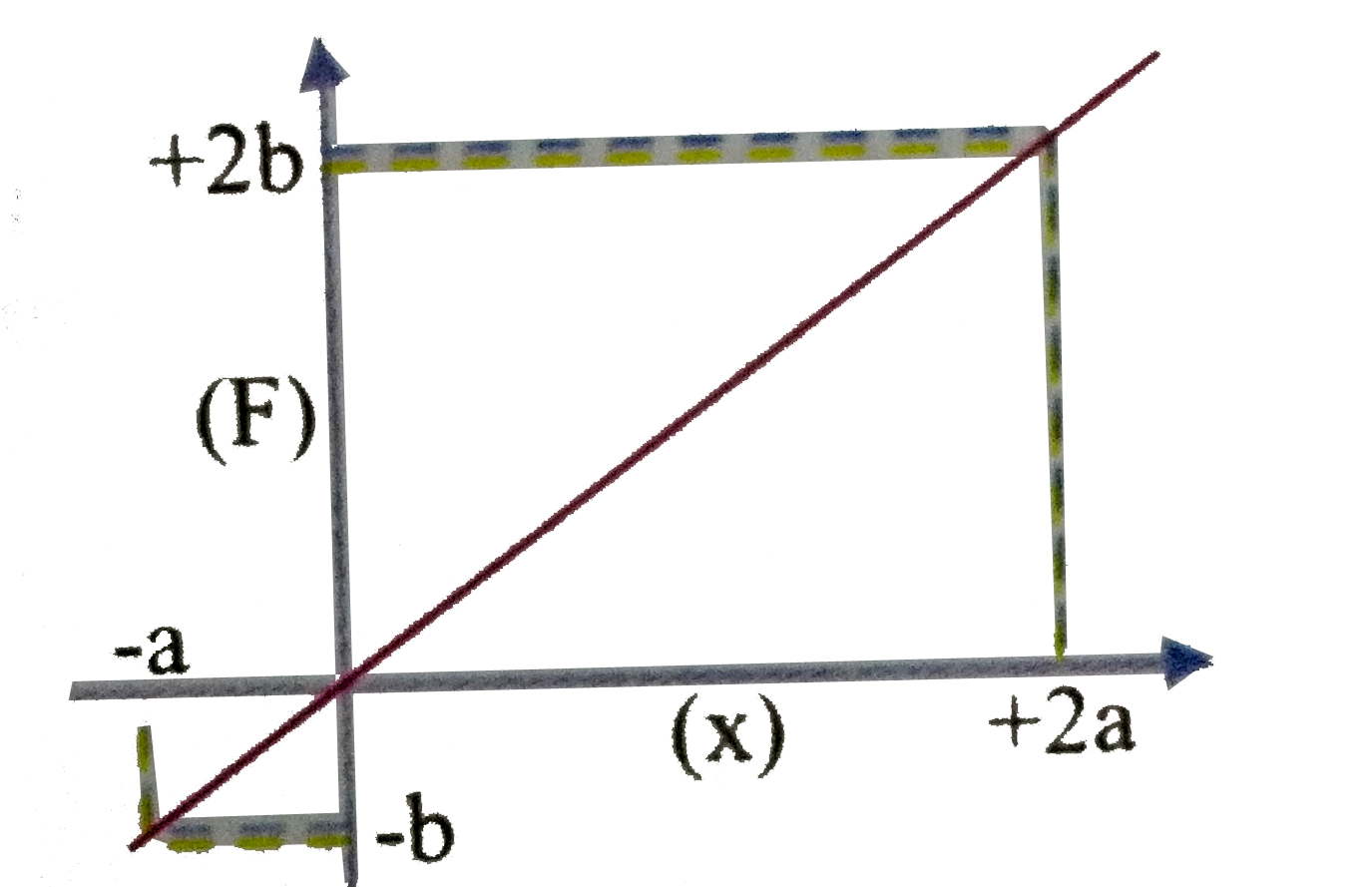 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
A force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force F=(a+bx) acts on a particle in x direction where a and b are constants . Find the work done by this force during displacement from x1 to x2 .
View SolutionA force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
View SolutionA force f=10+2x acts on a particle moving in straight line on x axis the work done by this force during a displacement from x=0 and x=3m
View SolutionThe force acting on a bod moving parallel to the X-axis is F=3x+2x2. What is the work done in displacing the body from x=1 to x=2?
View Solution

