A mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
1kg
2kg
3kg
4kg
The correct Answer is:C
f1=12π√Km1
f2=12π√Km2
f2=f12 or m2=4m1 or m2−m1=kg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - I
Explore 26 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 2, PART - II
Explore 1 Video
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Exercise- 1, PART - I
Explore 25 Videos
- SEMICONDUCTORSBook:RESONANCEChapter:SEMICONDUCTORSExercise:Exercise 3
Explore 88 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:FST-3
Explore 30 Videos
Similar Questions
Knowledge Check
Ultrasound has frequency of vibration
Abetween 20 and 20,000 HzBbelow 20 HzCabove 20,000 HzDbetween 500 and 10,000 HzUltrasound has frequency of vibration
A20 HzBbetween 20 to 20,000 HzCabove 20,000 HzDless than 20 HzWhich of the following tools has a spring attached to it?
AHacksawBViceCTin cutterDDrilin
A mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
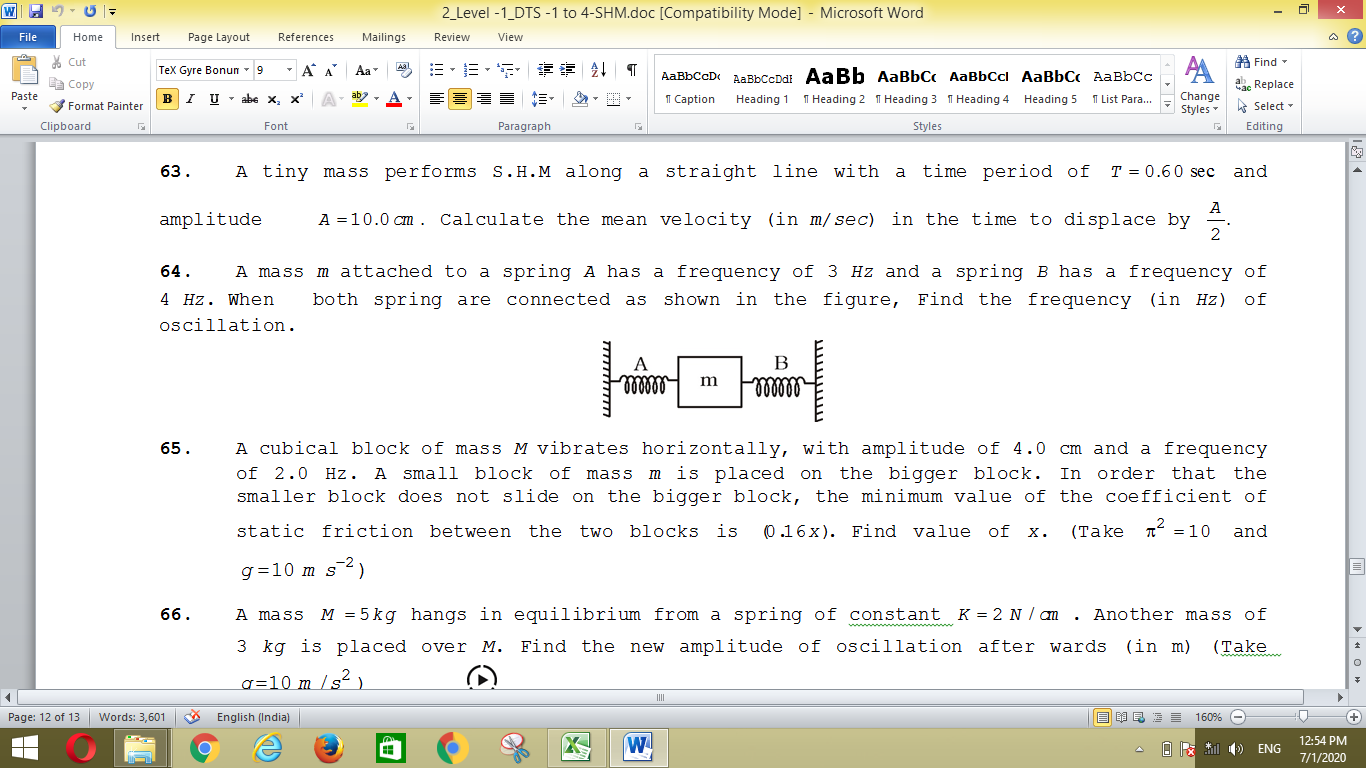
View SolutionOn suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :

View SolutionWhich of the following tools has a spring attached to it?
View SolutionA mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is f1. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is f2 . Which of the following relations between the frequencies is correct
View SolutionA spring mass system oscillates with a frequency n .If it is taken in an elavator slowly accelerating upward, the frequency will
View Solution