A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
The correct Answer is:9 rpm
To solve the problem, we will use the principle of conservation of angular momentum. The angular momentum of a system remains constant if no external torque acts on it.
1. Identify Initial Conditions:
- Mass of the platform (M) = 200 kg
- Mass of the boy (m) = 80 kg
- Initial angular speed (ω_initial) = 5 rpm
2. Convert Angular Speed to Radians per Second:
- Since 1 rpm = 2π60 rad/s, we convert 5 rpm to rad/s:
ωinitial=5×2π60=5π30=π6 rad/s
3. Calculate Initial Moment of Inertia:
- The moment of inertia of the platform (I_platform) is given by:
Iplatform=12MR2
- The boy is initially at the edge, so his moment of inertia (I_boy_initial) is:
Iboy initial=mR2
- Total initial moment of inertia (I_initial):
Iinitial=Iplatform+Iboy initial=12MR2+mR2=(12×200+80)R2=(100+80)R2=180R2
4. Calculate Initial Angular Momentum:
- Angular momentum (L_initial) is given by:
Linitial=Iinitial⋅ωinitial=180R2⋅π6=30πR2
5. Calculate Final Moment of Inertia:
- When the boy moves to the center, his moment of inertia becomes zero (I_boy_final = 0). Therefore, the final moment of inertia (I_final) is:
Ifinal=Iplatform+Iboy final=12MR2+0=12×200R2=100R2
6. Apply Conservation of Angular Momentum:
- According to the conservation of angular momentum:
Linitial=Lfinal
- Thus,
30πR2=100R2⋅ωfinal
7. Solve for Final Angular Speed (ω_final):
- Dividing both sides by R2 (assuming R≠0):
30π=100ωfinal
- Therefore,
ωfinal=30π100=3π10 rad/s
Final Answer:
The final angular speed of the platform after the boy moves to the center is 3π10 rad/s.
- Mass of the platform (M) = 200 kg
- Mass of the boy (m) = 80 kg
- Initial angular speed (ω_initial) = 5 rpm
- Since 1 rpm = 2π60 rad/s, we convert 5 rpm to rad/s:
ωinitial=5×2π60=5π30=π6 rad/s
- The moment of inertia of the platform (I_platform) is given by:
Iplatform=12MR2
- The boy is initially at the edge, so his moment of inertia (I_boy_initial) is:
Iboy initial=mR2
- Total initial moment of inertia (I_initial):
Iinitial=Iplatform+Iboy initial=12MR2+mR2=(12×200+80)R2=(100+80)R2=180R2
- Angular momentum (L_initial) is given by:
Linitial=Iinitial⋅ωinitial=180R2⋅π6=30πR2
- When the boy moves to the center, his moment of inertia becomes zero (I_boy_final = 0). Therefore, the final moment of inertia (I_final) is:
Ifinal=Iplatform+Iboy final=12MR2+0=12×200R2=100R2
- According to the conservation of angular momentum:
Linitial=Lfinal
- Thus,
30πR2=100R2⋅ωfinal
- Dividing both sides by R2 (assuming R≠0):
30π=100ωfinal
- Therefore,
ωfinal=30π100=3π10 rad/s
The final angular speed of the platform after the boy moves to the center is 3π10 rad/s.
Topper's Solved these Questions
Similar Questions
A horizontal platform with a mass of 100kg rotates at 10(r±) around a vertical axis passing through its centre. A man of mass 60kg is standing on its edge. The platform begins to rotaté with an angular velocity ω(r±), if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of 3ω11.
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View Solution
Knowledge Check
A uniform horizontal circular platform of mass 200kg is rotating at 10 rpm about a vertical axis passing through its center. A boy of mass 50kg is standing at its edge. If the boy moves to the center of the platform, the frequency of rotation would become
A7.5 rpmB12.5 rpmC15 rpmD20 rpmA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0 . When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as
A B
B C
C D
D
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform Now, the platform is given an angular velocity ω0. When the tortoise moves along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform will vary with time t as -
A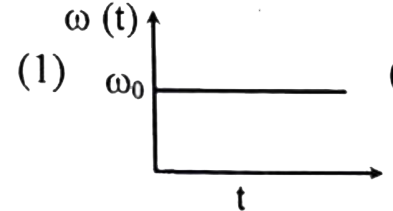 B
B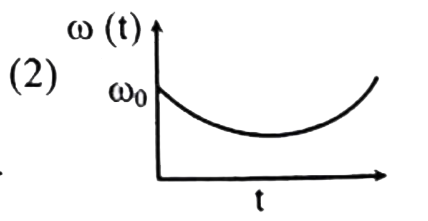 C
C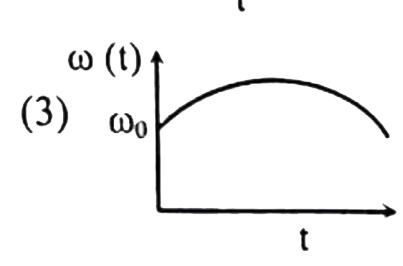 D
D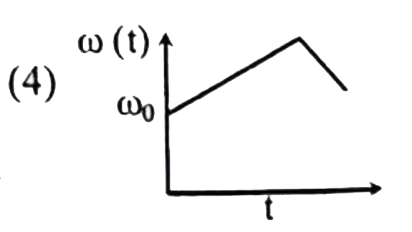
A circular plarform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its center. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity c.o0. When the tortoise moves along the diameter of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View Solution
