A uniform horizontal circular platform of mass 200kg is rotating at 10 rpm about a vertical axis passing through its center. A boy of mass 50kg is standing at its edge. If the boy moves to the center of the platform, the frequency of rotation would become
7.5 rpm
12.5 rpm
15 rpm
20 rpm
To solve the problem, we need to apply the principle of conservation of angular momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
We have a circular platform with a mass of 200 kg rotating at 10 revolutions per minute (rpm). A boy with a mass of 50 kg is standing at the edge of the platform.
Step 2: Calculate Initial Moment of Inertia
The moment of inertia (I) of the system before the boy moves can be calculated as follows:
1. Moment of Inertia of the Boy (at the edge):
Iboy=mboy⋅r2=50⋅R2
where R is the radius of the platform.
2. Moment of Inertia of the Platform:
Iplatform=12mplatform⋅R2=12⋅200⋅R2=100R2
3. Total Initial Moment of Inertia:
Iinitial=Iboy+Iplatform=50R2+100R2=150R2
Step 3: Calculate Initial Angular Velocity
Convert the initial angular velocity from rpm to radians per second:
ωinitial=10 rpm=10⋅2π rad1 min=10⋅2π60 rad/s=10π30=π3 rad/s
Step 4: Calculate Final Moment of Inertia
When the boy moves to the center of the platform, his moment of inertia becomes zero because he is at the axis of rotation. Thus, the final moment of inertia is just that of the platform:
Ifinal=Iplatform=100R2
Step 5: Apply Conservation of Angular Momentum
According to the conservation of angular momentum:
Linitial=Lfinal
This can be expressed as:
Iinitial⋅ωinitial=Ifinal⋅ωfinal
Substituting the values we have:
150R2⋅π3=100R2⋅ωfinal
Step 6: Solve for Final Angular Velocity
We can cancel R2 from both sides:
150⋅π3=100⋅ωfinal
Now, simplify:
50π=100⋅ωfinal
ωfinal=50π100=π2 rad/s
Step 7: Convert Final Angular Velocity to RPM
Convert back to rpm:
ωfinal=π2 rad/s=π2⋅602π rpm=15 rpm
Final Answer
The final frequency of rotation when the boy moves to the center of the platform is 15 rpm.
---
We have a circular platform with a mass of 200 kg rotating at 10 revolutions per minute (rpm). A boy with a mass of 50 kg is standing at the edge of the platform.
The moment of inertia (I) of the system before the boy moves can be calculated as follows:
Iboy=mboy⋅r2=50⋅R2
where R is the radius of the platform.
Iplatform=12mplatform⋅R2=12⋅200⋅R2=100R2
Iinitial=Iboy+Iplatform=50R2+100R2=150R2
Convert the initial angular velocity from rpm to radians per second:
ωinitial=10 rpm=10⋅2π rad1 min=10⋅2π60 rad/s=10π30=π3 rad/s
When the boy moves to the center of the platform, his moment of inertia becomes zero because he is at the axis of rotation. Thus, the final moment of inertia is just that of the platform:
Ifinal=Iplatform=100R2
According to the conservation of angular momentum:
Linitial=Lfinal
This can be expressed as:
Iinitial⋅ωinitial=Ifinal⋅ωfinal
Substituting the values we have:
150R2⋅π3=100R2⋅ωfinal
We can cancel R2 from both sides:
150⋅π3=100⋅ωfinal
Now, simplify:
50π=100⋅ωfinal
ωfinal=50π100=π2 rad/s
Convert back to rpm:
ωfinal=π2 rad/s=π2⋅602π rpm=15 rpm
The final frequency of rotation when the boy moves to the center of the platform is 15 rpm.
Topper's Solved these Questions
Similar Questions
A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA horizontal platform with a mass of 100kg rotates at 10(r±) around a vertical axis passing through its centre. A man of mass 60kg is standing on its edge. The platform begins to rotaté with an angular velocity ω(r±), if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of 3ω11.
View Solution
Knowledge Check
A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all pointsBdifferent at differen points and maximum at centre of rodCdifferent at different points and minimum at axis of rotation.Ddifferent at different points and maximum at axis of rotationA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
A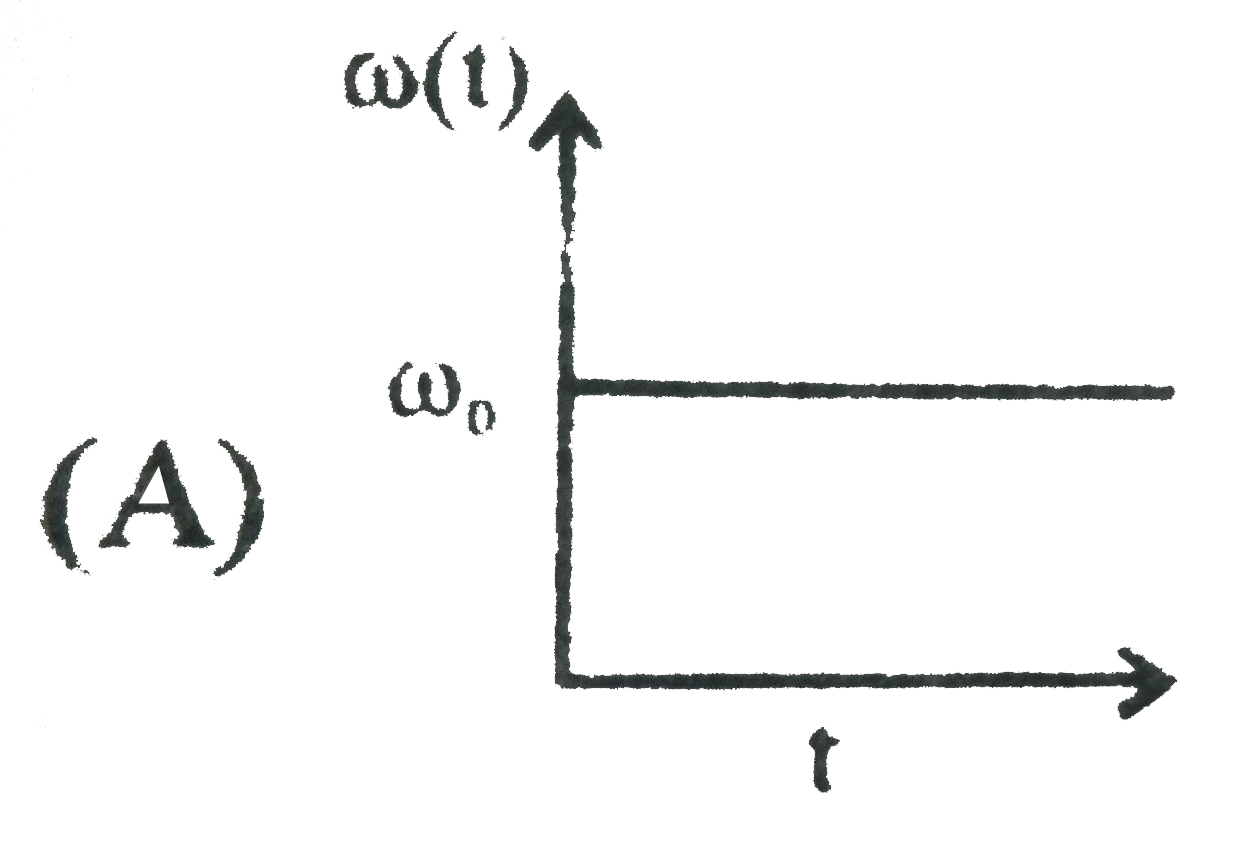 B
B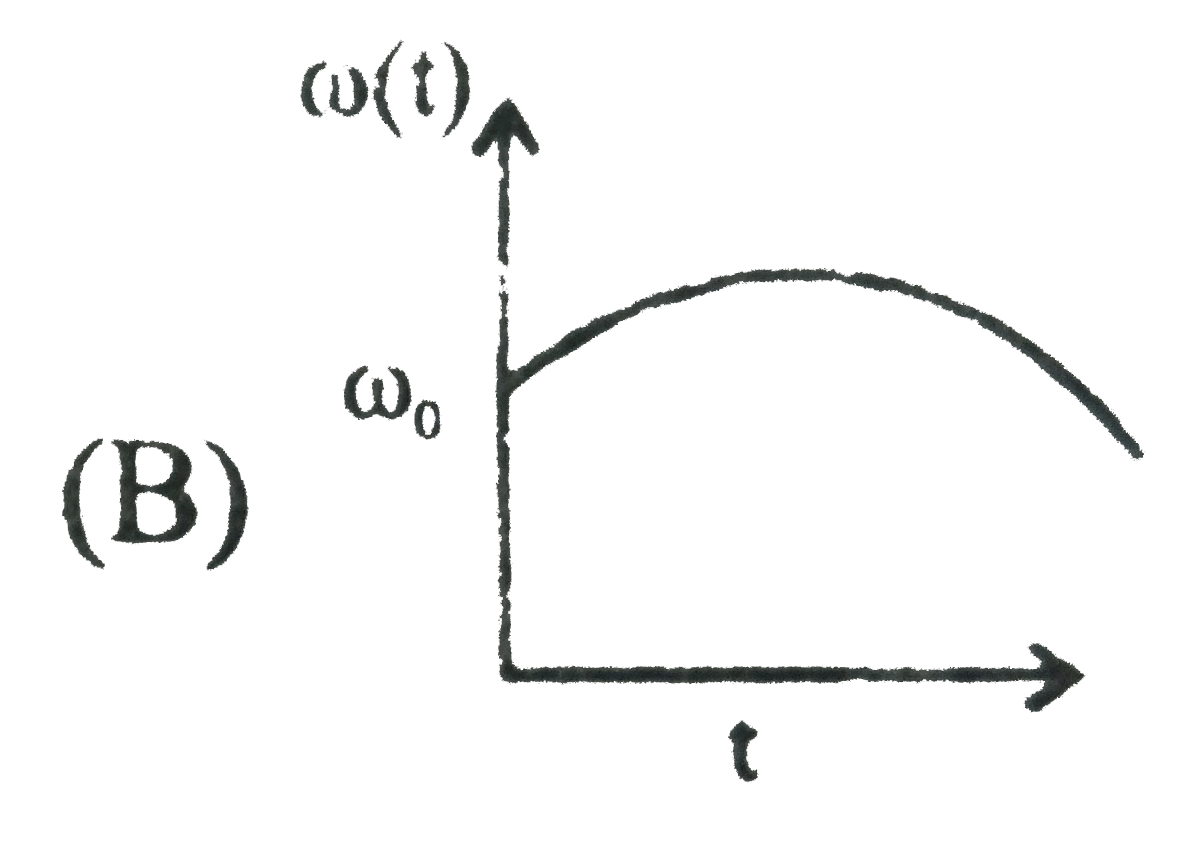 C
C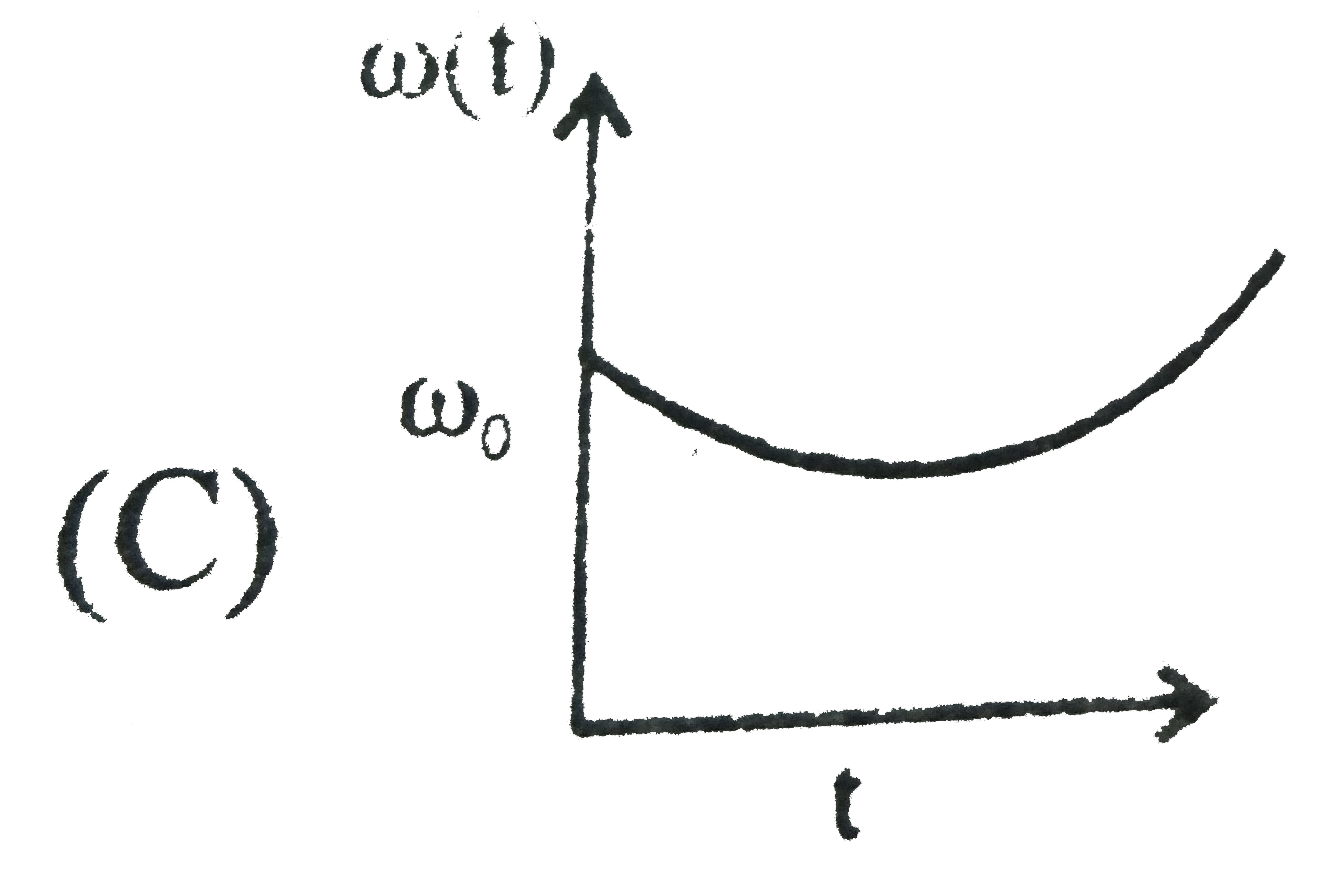 D
D
A uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
Aw06Bw05C4ω05D5ω06
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its center. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity c.o0. When the tortoise moves along the diameter of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as
View SolutionA circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View Solution

