A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
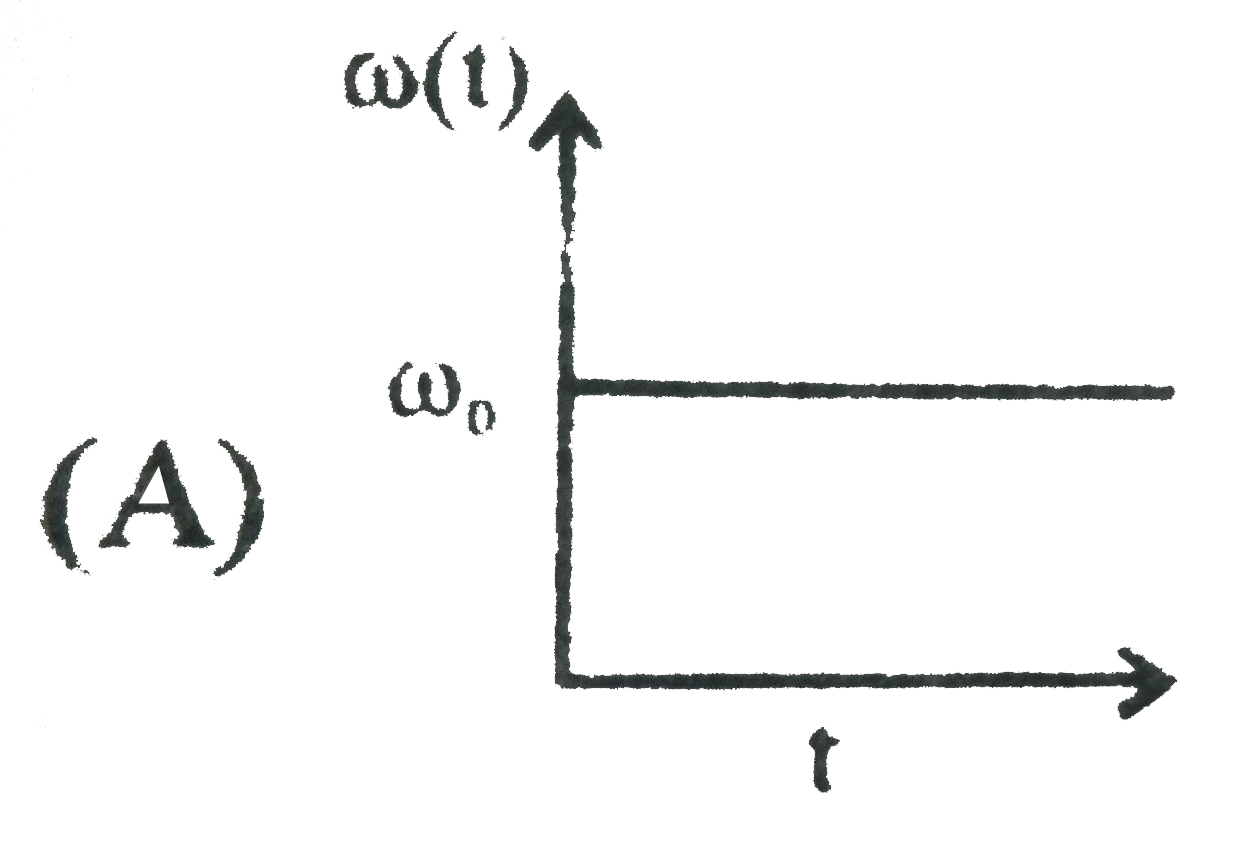
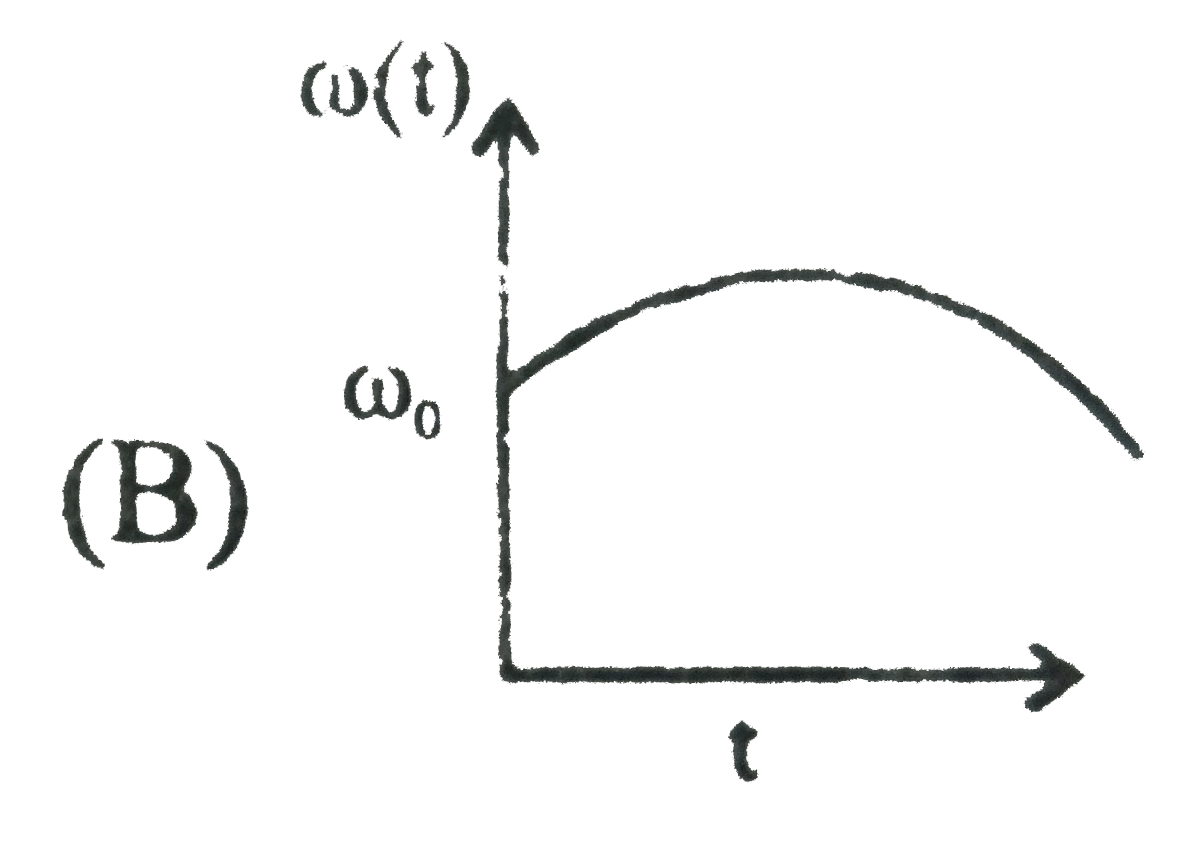
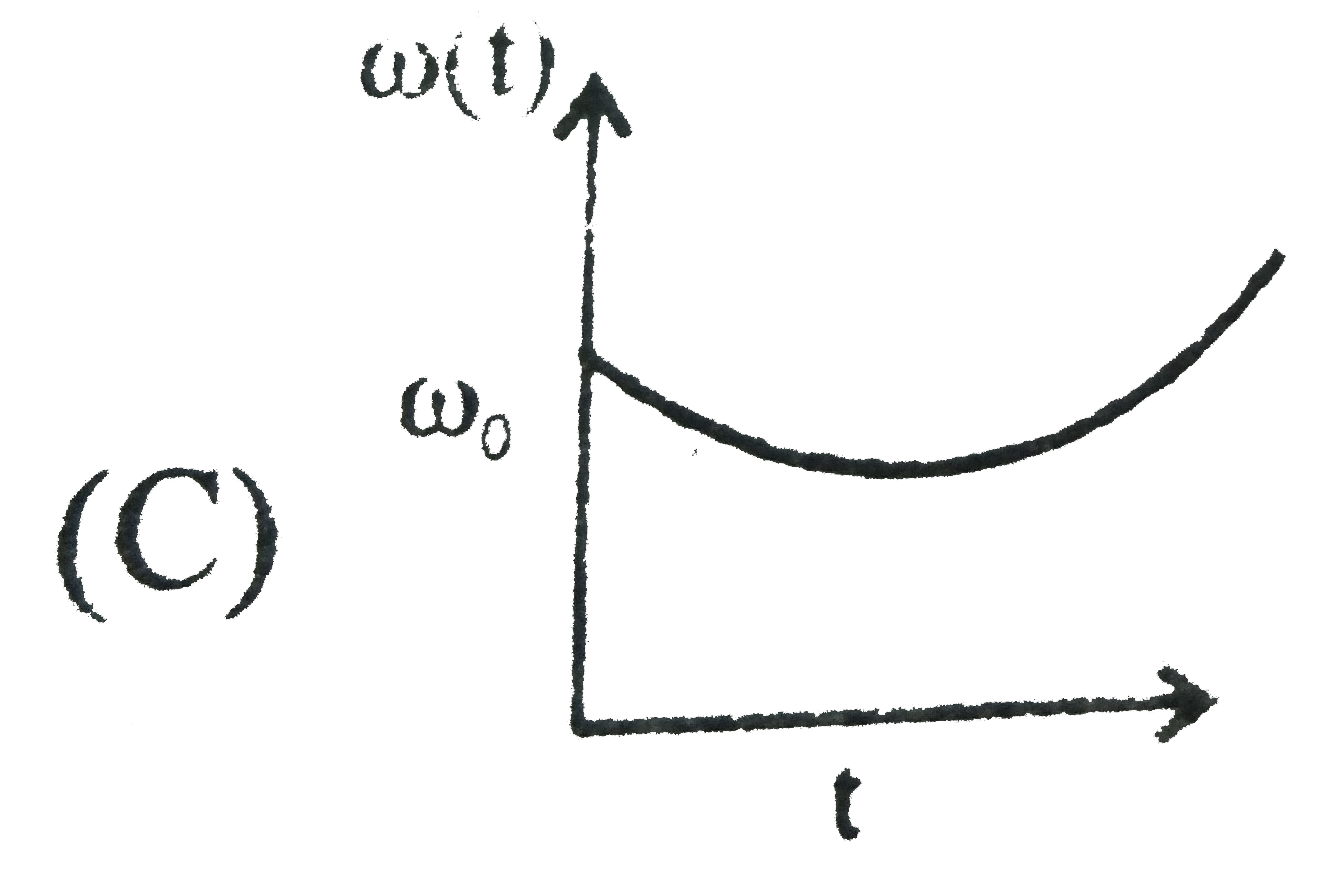

The correct Answer is:B
Since, there is no external torque, angular momentum will remain conserved. The momentum will remain conserved. The moment of inertia will first decreases till the tortise moves from A to C and then increases as it moves from A to C and then increases as it moves from C to D. Therefore,ω will initially increases and then decrease. Let R be the radius of platform, m the mass of disc and M is the mass of platform.
moment of inertia when the tortoise is at A
I1=mR2+MR22
and moment of inertia when the torroise is at B
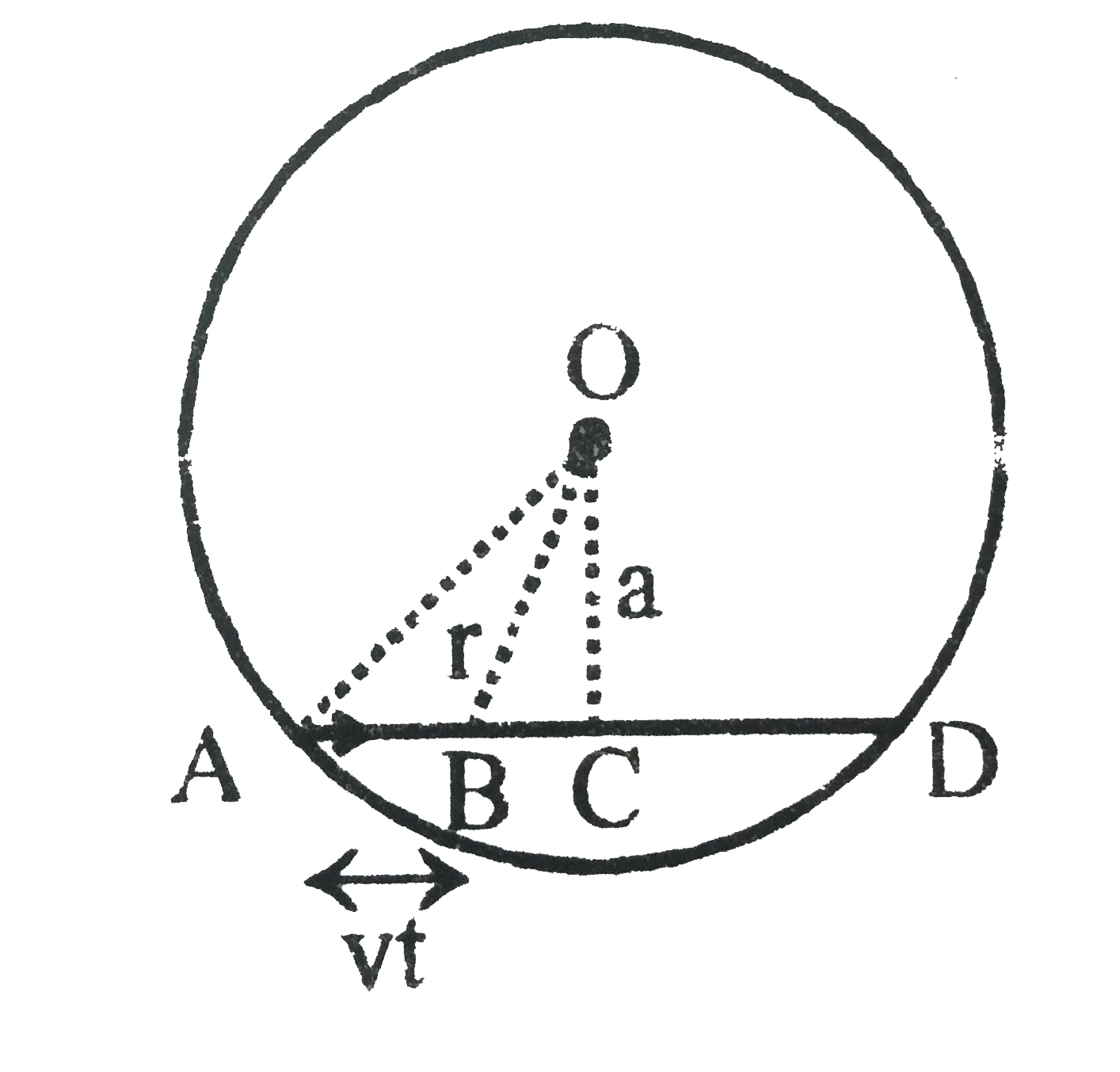
I2=mr2+MR22
here, r2=a2+[√R2−a2−vt]2
From conservation of angular momentum
ω0I1=ω(t)I2
Sustituting the values we can see the variation of ω(t) is non-linear.
Similar Questions
A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA horizontal platform with a mass of 100kg rotates at 10(r±) around a vertical axis passing through its centre. A man of mass 60kg is standing on its edge. The platform begins to rotaté with an angular velocity ω(r±), if the man "moves from the edge of the platform to its centre. Regard the platform as a circular homogeneous disk and the man as a point mass. Find the value of 3ω11.
View Solution
Knowledge Check
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its centre. A tortoise is sitting at the edge of the platform. Now the platform is given an angular velocity ω0. When the tortoise move along a chord of the platform with a constant velocity (with respect to the platform),
A B
B C
C D
D
A circular platform is free to rotate in a horizontal plane about a vertical axis passing through its center. A tortoise is sitting at the edge of the platform. Now, the platform is given an angular velocity c.o0. When the tortoise moves along the diameter of the platform with a constant velocity (with respect to the platform), the angular velocity of the platform ω(t) will vary with time t as
A B
B C
C D
D
A circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
AincreasesBdecreasesCdoes not changeDbecomes zero
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionAn ice block is in a trough which is rotating about vertical axis passing through its centre. When ice melts completely, the angular velocity of the system
View SolutionA uniform horizontal circular platform of mass 200kg is rotating at 10 rpm about a vertical axis passing through its center. A boy of mass 50kg is standing at its edge. If the boy moves to the center of the platform, the frequency of rotation would become
View Solution
A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given as
View Solution

