The hollow cylinder of length l and inner and outer radius R1 and R2 respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id ρ .
((ρπelln(R1R2))
((ρ4πelln(R2R1))
((ρ3πelln(R2R1))
((ρ2πelln(R2R1))
The correct Answer is:D
To find the resistance of a hollow cylinder with inner radius R1, outer radius R2, length L, and resistivity ρ, we can follow these steps:
1. Understand the Geometry:
- We have a hollow cylinder with inner radius R1 and outer radius R2. The current flows radially outward from the inner surface to the outer surface.
2. Define the Resistance Formula:
- The resistance R of a conductor is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length of the conductor, and A is the cross-sectional area through which the current flows.
3. Identify the Length and Area:
- For a thin cylindrical shell at a radius r with thickness dr:
- The length L of the cylinder remains constant.
- The cross-sectional area A for the current flowing through this shell is the circumference of the shell times its length:
A=2πrL
4. Calculate the Resistance of the Thin Shell:
- The resistance dR of a thin shell of thickness dr at radius r is given by:
dR=ρdrA=ρdr2πrL
5. Integrate to Find Total Resistance:
- To find the total resistance R of the hollow cylinder, integrate dR from R1 to R2:
R=∫R2R1dR=∫R2R1ρdr2πrL
- This simplifies to:
R=ρ2πL∫R2R1drr
- The integral ∫drr evaluates to ln(r):
R=ρ2πL(ln(r))R2R1=ρ2πL(ln(R2)−ln(R1))
6. Final Expression:
- Using the properties of logarithms, this can be expressed as:
R=ρ2πLln(R2R1)
Final Result:
R=ρ2πLln(R2R1)
- We have a hollow cylinder with inner radius R1 and outer radius R2. The current flows radially outward from the inner surface to the outer surface.
- The resistance R of a conductor is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length of the conductor, and A is the cross-sectional area through which the current flows.
- For a thin cylindrical shell at a radius r with thickness dr:
- The length L of the cylinder remains constant.
- The cross-sectional area A for the current flowing through this shell is the circumference of the shell times its length:
A=2πrL
- The resistance dR of a thin shell of thickness dr at radius r is given by:
dR=ρdrA=ρdr2πrL
- To find the total resistance R of the hollow cylinder, integrate dR from R1 to R2:
R=∫R2R1dR=∫R2R1ρdr2πrL
- This simplifies to:
R=ρ2πL∫R2R1drr
- The integral ∫drr evaluates to ln(r):
R=ρ2πL(ln(r))R2R1=ρ2πL(ln(R2)−ln(R1))
- Using the properties of logarithms, this can be expressed as:
R=ρ2πLln(R2R1)
R=ρ2πLln(R2R1)
Topper's Solved these Questions
Similar Questions
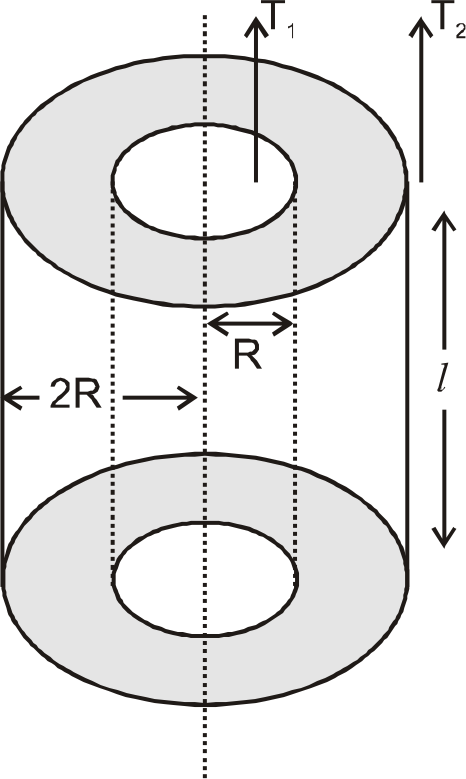
Inner surfaec of a cylindrical shell of length l and of material of thermal conductivity k is kept at constant temperature T1 and outer surface of the cylinder is kept at constant temperature T2 such that (T1>T2) as shown in figure. heat flows from inner surface to outer surface radially outward. inner and outer radii of the shell are R and 2R resspectively. Due to lack of space this cylinder has to be replaced by a smaller cylinder of length l2 inner and outer radii R4 and R respectively and thermal conductivity of material nk. if rate of radially outward heat flow remains same for same temperatures of inner and outer surface i.e., T1 and T2 then find the value of n.
View SolutionWhat is the volume of a hollow cylinder with R, r and h as outer radius, inner radius and height respectively?
View Solution
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is ρ. The resistance of the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρlA hollow cylinder of infinite length carries a current I as shown. Magnetic field inside the cylinder is
 Aμ0l2πdBμ0l4πdCμ0l2πR2dDzero
Aμ0l2πdBμ0l4πdCμ0l2πR2dDzeroA resistor is constructed as hollow cylinder with inner and outer radii ra=0.5cm,rb=1.0 cm respectively and resistivity ρ=3.5×10−5Ω. The resistance of the configuration for the length of 5 cm cylinder is _______×10−3Ω.
A7.42B10.56C14.38D16.48
The external and the internal radii of a hollow right circular cylinder of height 15 cm are 6.75 cm and 5.25 cm respectively. If it is melted to form a solid cylinder of height half of the orignal cylinder, then the radius of the solid cylinder is-
View SolutionA hollow cylinder of length l and of radii a and b is filled with a material of resistivity ρ and is connected to a battery of emf E through an ammeter. Find the current through ammeter

View SolutionThe inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
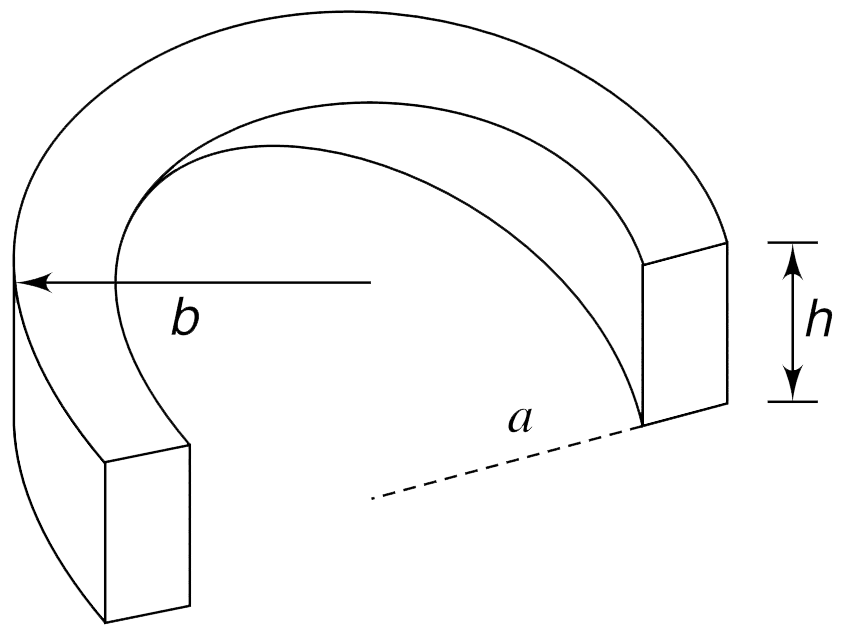
View SolutionA conductor having resistivity ρ is bent in the shape of a half cylinder as shown in the figure. The inner and outer radii of the cylinder are aandb respectively and the height of the cylinder is h. A potential difference is applied across the two rectangular faces of the conductor. Calculate the resistance offered by the conductor.
View SolutionThe length and radius of a cylinder are L and R respectively. The total flux for the surface of the cylinder, when it is placed in a uniform electric field E parallel to the axis of the cylinder is
View Solution

