A mas m is moving in SHM on a line with amplitude A and frequency f. suddenly half of the mass comes to rest just at the moment when it comes mean position then the new amplitude becomes λA, then λ will be
43832
1√2
√2
1
The correct Answer is:C
To solve the problem, we will analyze the situation step by step, using the principles of simple harmonic motion (SHM) and conservation of momentum.
Step 1: Understanding the Initial Conditions
We have a mass m moving in simple harmonic motion (SHM) with an amplitude A and frequency f. The mass oscillates due to a spring with spring constant k.
Hint: Remember that the frequency of SHM is related to the mass and spring constant by the formula f=12π√km.
Step 2: Determine the Initial Angular Frequency
The angular frequency ω1 of the mass m is given by:
ω1=√km
Hint: The angular frequency is a measure of how quickly the mass oscillates.
Step 3: Analyze the Change in Mass
When half of the mass (m/2) comes to rest at the mean position, the remaining mass that continues to oscillate is m/2. The new angular frequency ω2 for the remaining mass is:
ω2=√km/2=√2km=√2⋅√km=√2⋅ω1
Hint: When the mass changes, the new angular frequency can be derived from the original frequency by considering the new effective mass.
Step 4: Relate the Velocities at the Mean Position
At the mean position, the velocity of the mass can be expressed as:
v1=ω1A
for the original mass m, and for the new mass m/2:
v2=ω2A2
where A2 is the new amplitude we need to find.
Hint: The velocity at the mean position is maximum and is directly proportional to the amplitude.
Step 5: Apply Conservation of Momentum
Since no external forces act on the system, we can apply the conservation of momentum. The momentum before half the mass comes to rest is equal to the momentum after:
mv1=m2v2
Substituting the velocities:
m(ω1A)=m2(ω2A2)
Hint: The conservation of momentum principle states that the total momentum before an event must equal the total momentum after the event.
Step 6: Substitute the Angular Frequencies
Substituting ω1 and ω2:
m(√kmA)=m2(√2⋅√kmA2)
This simplifies to:
√kmA=m2√2⋅√kmA2
Step 7: Cancel and Rearrange
Cancel m and √k:
A=12√2A2
Rearranging gives:
A2=2A√2=√2A
Step 8: Find the Value of λ
From the problem, we know that:
A2=λA
Thus, we have:
λA=√2A
This leads to:
λ=√2
Final Answer
The value of λ is √2.
---
We have a mass m moving in simple harmonic motion (SHM) with an amplitude A and frequency f. The mass oscillates due to a spring with spring constant k.
The angular frequency ω1 of the mass m is given by:
ω1=√km
When half of the mass (m/2) comes to rest at the mean position, the remaining mass that continues to oscillate is m/2. The new angular frequency ω2 for the remaining mass is:
ω2=√km/2=√2km=√2⋅√km=√2⋅ω1
At the mean position, the velocity of the mass can be expressed as:
v1=ω1A
for the original mass m, and for the new mass m/2:
v2=ω2A2
where A2 is the new amplitude we need to find.
Since no external forces act on the system, we can apply the conservation of momentum. The momentum before half the mass comes to rest is equal to the momentum after:
mv1=m2v2
Substituting the velocities:
m(ω1A)=m2(ω2A2)
Substituting ω1 and ω2:
m(√kmA)=m2(√2⋅√kmA2)
This simplifies to:
√kmA=m2√2⋅√kmA2
Cancel m and √k:
A=12√2A2
Rearranging gives:
A2=2A√2=√2A
From the problem, we know that:
A2=λA
Thus, we have:
λA=√2A
This leads to:
λ=√2
The value of λ is √2.
Topper's Solved these Questions
Similar Questions
A block of mass m attached to a massless spring is performing oscillatory motion of amplitude A on a frictionless horizontal plane. If half of the mass of the block off when it is passing through its mean position, the amplitude of oscillation for the remaining system become fA. The value of f is .
View SolutionA block of mass M executes SHM with amplitude a and time period T. When it passes through the mean position, a lump of putty of mass m is dropped on it. Find the new amplitude and time period.
View Solution
Knowledge Check
A particle of mass 1 kg is moving in SHM with an amplitude 0.02 m and a frequency of 60 Hz. The maximum force (in N) acting on the particle is
A188 π2B144 π2C288 π2DNone of the aboveA particle of mass m performs SHM along a stright line with frequency f and amplitude A.
AThe average kenetic energy of the particle is zero.BThe average potential energy is mπ2f2A2.CThe frequency of ocillation of kinetic energy is 2f.DVelocity funciton leads acceleration by π/2.A particle of mass m performs SHM along a straight line with frequency f and amplitude A:-
AThe average kinetic energy of the particle is zeroBThe average potential energy is mπ2f2A2CThe frequency of oscillation of kinetic energy is 2fDVelocity function leads acceleration by π/2
A block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
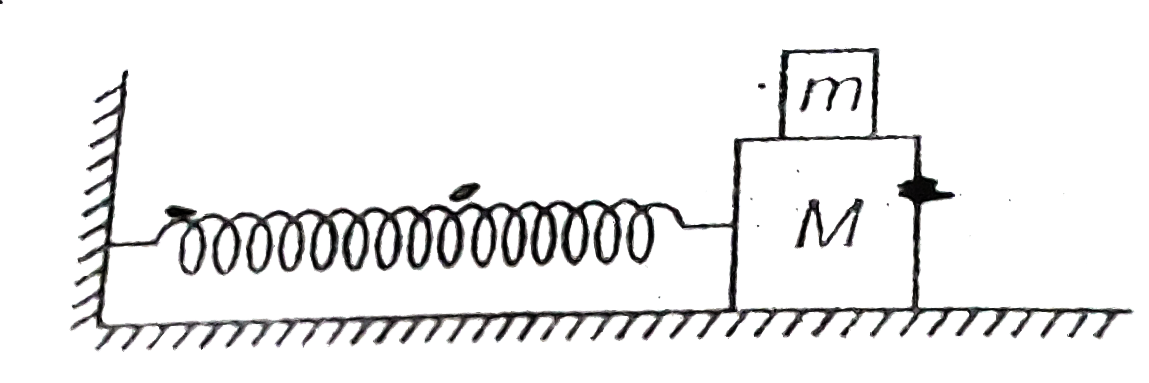
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
View SolutionBlock A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionAn object of mass M oscillating with amplitude 'A' mass 'm' is added at mean position. Find new amplitude of oscillation.
View Solutionparticle is executing SHM of amplitude A and angular frequency omega.The average acceleration of particle for half the time period is : (Starting from mean position)
View SolutionA particle of mass m executes SHM with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilibrium to the end is
View Solution
