Mass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field 
4π3(Gρ0R)
2π√35(Gρ0R)
8π√527(Gρ0R)
2π√527(Gρ0R)
The correct Answer is:C
Step by step video, text & image solution for Mass density of sphere having radius R varies as rho = rho_0(1-r^2/R^2) . Find maxium magnitude of gravitational field by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionThe volume charge density inside of sphere of radius R is given by ρ=ρ0(1−rR) ,where ρ0 is constant and r distance from centre.
(a) Find total charge Q inside sphere.
Electric field outside sphere at distance r from centre.
(b) Electric field outside sphere at distance r from centre.
(c) Electric field inside sphere at distance r from centre.
(d) At what distance from centre electric field is maximum and its value?
(e ) Sketch E versus r graph.
View Solution
Knowledge Check
Charge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2
AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2An infinite cylindrical wire of radius R and having current density varying with its radius r as, J=J0[1−(r/R)]. Then answer the following questions.
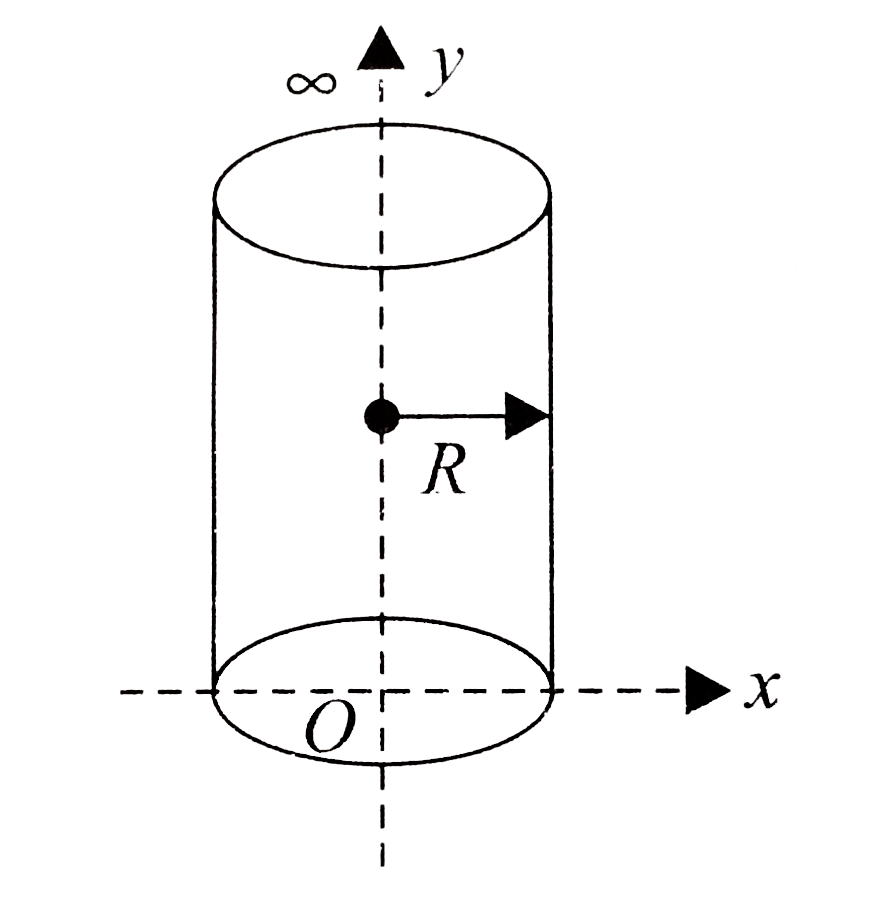
Magnitude of maximum magnetic field isAJ0R6μ0B316J0Rμ0C516J0Rμ0D56J0Rμ0
A non-conducting sphere of radius R has a spherical cavity of radius R/2 as shown. The solid part of the sphere has a uniform volume charge density ρ. Find the magnitude and direction of electric field at point (a) O and (b) A.

View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionA sphere of radius R has its centre at the origin. It has a uniform mass density ρ0 except that there is a spherical hole of radius r=R/2 whose centre is at x=R/2 as in fig (a) find gravitational field at points on the axis for x>R (ii) Show that the gravitational field inside the hole is uniform, find its magnitude and direction.

View SolutionConsider a solid sphere oFIGURE radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oFIGURE a liquid in which it will FIGUREloat is:
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionA solid sphere of radius R and mass density ρ is surrounded by another outer sphere of density 2ρ. Let EP is gravitational field at P and EQ is at Q. If the ratio of EQ/EP=3k/4. Find the value of k.

View Solution