Question

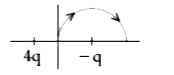
Two charges 4q and -q are kept on x-axis at $(-\frac{d}{2},0)$ and $(\frac{d}{2},0)$ resp. Then charge +q is moved from origin to x=d via semicircular path . Find change in its energy.

Answer

A::C::D

Explanation

To find the change in energy when a charge +q is moved from the origin to x = d via a semicircular path in the presence of two other charges (4q at (-d/2, 0) and -q at (d/2, 0)), we can follow these steps:

Step 1: Understand the Initial Configuration
We have three charges:
- Charge 1: \(4q\) located at \((-d/2, 0)\)
- Charge 2: \(-q\) located at \((d/2, 0)\)
- Charge 3: \(+q\) initially at the origin \((0, 0)\)

Step 2: Calculate Initial Potential Energy (E1)
The potential energy of a system of point charges is given by the formula:
\( U = k \frac{q_1 q_2}{r} \)
where \(k\) is Coulomb's constant, \(q_1\) and \(q_2\) are the magnitudes of the charges, and \(r\) is the distance between them.

1. Potential Energy between Charge +q and Charge 4q:
- Distance from +q (at origin) to 4q (at -d/2) is \(d/2\).
- Potential Energy \(U_1 = k \frac{4q \cdot q}{d/2} = \frac{8kq^2}{d}\).

2. Potential Energy between Charge +q and Charge -q:
- Distance from +q (at origin) to -q (at d/2) is \(d/2\).
- Potential Energy \(U_2 = k \frac{-q \cdot q}{d/2} = -\frac{2kq^2}{d}\).

3. Total Initial Potential Energy (E1):
\( E_1 = U_1 + U_2 = \frac{8kq^2}{d} - \frac{2kq^2}{d} = \frac{6kq^2}{d} \)

Step 3: Calculate Final Potential Energy (E2)
Now we need to calculate the potential energy when the charge +q is moved to \(x = d\).

1. Potential Energy between Charge +q (at d) and Charge 4q:
- Distance from +q (at d) to 4q (at -d/2) is \(d + d/2 = \frac{3d}{2}\).
- Potential Energy \(U_3 = k \frac{4q \cdot q}{3d/2} = \frac{8kq^2}{3d}\).

2. Potential Energy between Charge +q (at d) and Charge -q:
- Distance from +q (at d) to -q (at d/2) is \(d - d/2 = \frac{d}{2}\).
- Potential Energy \(U_4 = k \frac{-q \cdot q}{d/2} = -\frac{2kq^2}{d}\).

3. Total Final Potential Energy (E2):
\( E_2 = U_3 + U_4 = \frac{8kq^2}{3d} - \frac{2kq^2}{d} \)
To combine these, convert \(-\frac{2kq^2}{d}\) to a common denominator:
\( -\frac{2kq^2}{d} = -\frac{6kq^2}{3d} \)
Thus,
\( E_2 = \frac{8kq^2}{3d} - \frac{6kq^2}{3d} = \frac{2kq^2}{3d} \)

Step 4: Calculate Change in Energy (ΔE)
The change in energy is given by:
\( \Delta E = E_2 - E_1 \)
Substituting the values we found:
\( \Delta E = \frac{2kq^2}{3d} - \frac{6kq^2}{d} \)
To combine these, convert \(\frac{6kq^2}{d}\) to a common denominator:
\( \frac{6kq^2}{d} = \frac{18kq^2}{3d} \)
Thus,
\( \Delta E = \frac{2kq^2}{3d} - \frac{18kq^2}{3d} = -\frac{16kq^2}{3d} \)

Step 5: Final Result
The change in energy when the charge +q is moved from the origin to \(x = d\) is:
\( \Delta E = -\frac{16kq^2}{3d} \)
If we substitute \(k = \frac{1}{4\pi \epsilon_0}\), we have:
\( \Delta E = -\frac{16}{3} \cdot \frac{1}{4\pi \epsilon_0} \cdot \frac{q^2}{d} \)