A circular disc of mass M and radius R rotating with speed of ω and another disc of same mass M and radius R/2 placed co axially on first disc, after sometime disc-2 also attain constant speed w2 . Find loss of percentage in energy
The correct Answer is:B
To solve the problem, we need to find the percentage loss of energy when a circular disc of mass M and radius R is rotating with an angular speed ω, and another disc of the same mass M and radius R2 is placed coaxially on the first disc. After some time, the second disc attains a constant angular speed ω2.
1. Calculate the Moment of Inertia of Each Disc:
- The moment of inertia I1 of the first disc (radius R):
I1=12MR2
- The moment of inertia I2 of the second disc (radius R2):
I2=12M(R2)2=12M⋅R24=18MR2
2. Initial Angular Momentum:
- The initial angular momentum Li of the system (only the first disc is rotating initially):
Li=I1ω=(12MR2)ω
3. Final Moment of Inertia of the Combined System:
- The total moment of inertia If when both discs are rotating together:
If=I1+I2=12MR2+18MR2=48MR2+18MR2=58MR2
4. Final Angular Momentum:
- The final angular momentum Lf when both discs are rotating with the final angular speed ω2:
Lf=Ifω2=(58MR2)ω2
5. Conservation of Angular Momentum:
- Since angular momentum is conserved:
Li=Lf
(12MR2)ω=(58MR2)ω2
- Cancel MR2 from both sides:
12ω=58ω2
- Solving for ω2:
ω2=45ω
6. Initial and Final Kinetic Energy:
- Initial kinetic energy Ei:
Ei=12I1ω2=12(12MR2)ω2=14MR2ω2
- Final kinetic energy Ef:
Ef=12Ifω22=12(58MR2)(45ω)2
Ef=12(58MR2)(1625ω2)=516MR2ω2
7. Calculate the Loss of Energy:
- Loss of energy ΔE:
ΔE=Ei−Ef=14MR2ω2−516MR2ω2
ΔE=(416−516)MR2ω2=−116MR2ω2
8. Percentage Loss of Energy:
- Percentage loss:
Percentage Loss=ΔEEi×100=−116MR2ω214MR2ω2×100=−11614×100=−116×4×100=−25%
- Since we are interested in the loss, we take the absolute value:
Percentage Loss=25%
Final Answer:
The percentage loss of energy is 25%.
- The moment of inertia I1 of the first disc (radius R):
I1=12MR2
- The moment of inertia I2 of the second disc (radius R2):
I2=12M(R2)2=12M⋅R24=18MR2
- The initial angular momentum Li of the system (only the first disc is rotating initially):
Li=I1ω=(12MR2)ω
- The total moment of inertia If when both discs are rotating together:
If=I1+I2=12MR2+18MR2=48MR2+18MR2=58MR2
- The final angular momentum Lf when both discs are rotating with the final angular speed ω2:
Lf=Ifω2=(58MR2)ω2
- Since angular momentum is conserved:
Li=Lf
(12MR2)ω=(58MR2)ω2
- Cancel MR2 from both sides:
12ω=58ω2
- Solving for ω2:
ω2=45ω
- Initial kinetic energy Ei:
Ei=12I1ω2=12(12MR2)ω2=14MR2ω2
- Final kinetic energy Ef:
Ef=12Ifω22=12(58MR2)(45ω)2
Ef=12(58MR2)(1625ω2)=516MR2ω2
- Loss of energy ΔE:
ΔE=Ei−Ef=14MR2ω2−516MR2ω2
ΔE=(416−516)MR2ω2=−116MR2ω2
- Percentage loss:
Percentage Loss=ΔEEi×100=−116MR2ω214MR2ω2×100=−11614×100=−116×4×100=−25%
- Since we are interested in the loss, we take the absolute value:
Percentage Loss=25%
The percentage loss of energy is 25%.
Topper's Solved these Questions
Similar Questions
A circular disc of mass M and radius R is rotating about its axis with angular speed If about another stationary disc having radius ω1.
R2 and same mass M is dropped co- axially on to the rotating disc. Gradually both discs attain constant angular speed ω2. The energy lost in the process is p% of the initial energy . Value of p is ........
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
A10 JB6 JC2 JD4 JA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
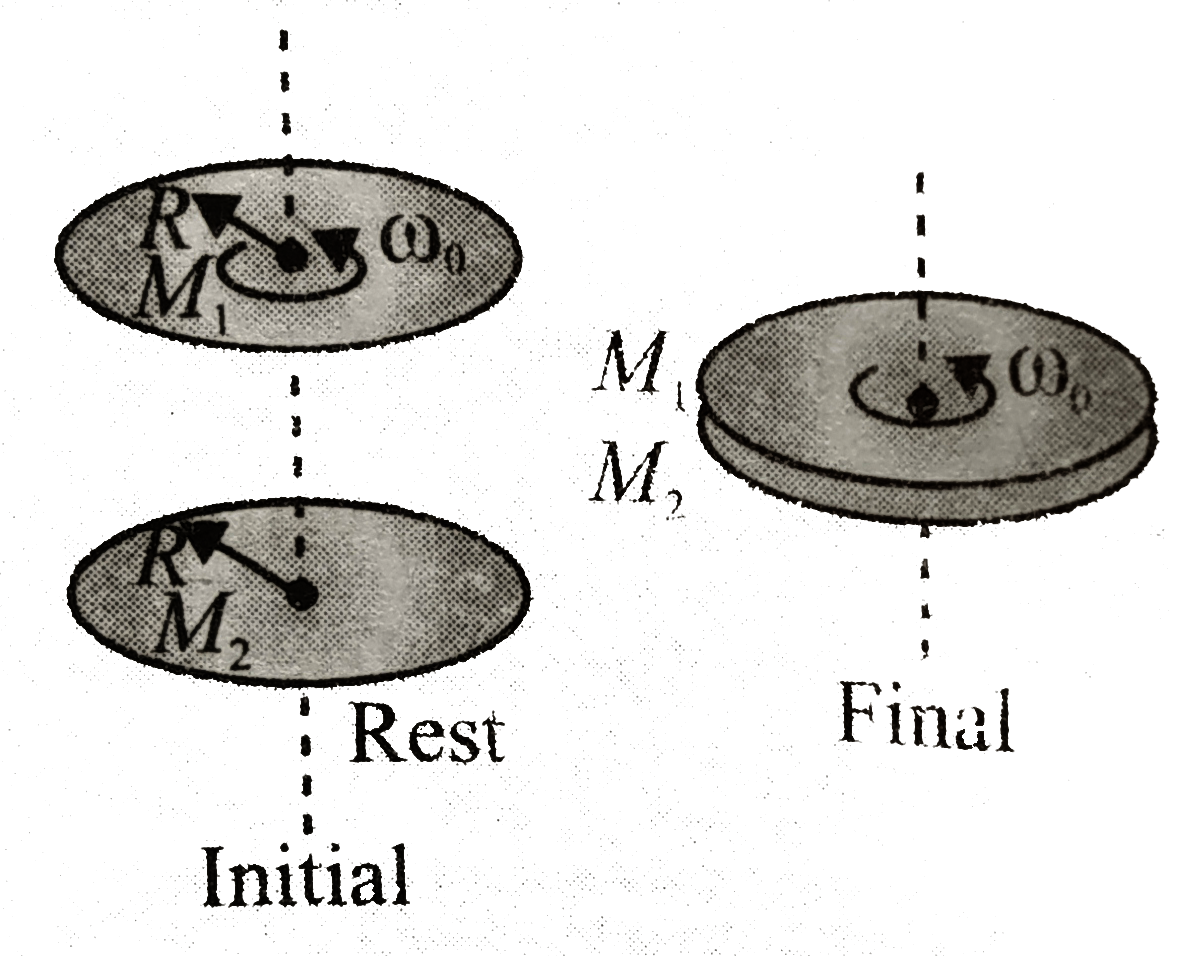 Am1m2Bm2m1+m2Cm2m1Dm1m1+m2
Am1m2Bm2m1+m2Cm2m1Dm1m1+m2A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ω
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA uniform disc of mass M and radius R is rotating in a horizontal plane about an axis perpendicular to its plane with an angular velocity ω. Another disc of mass M/3 and radius R/2 is placed gently on the first disc coaxial. Then final angular velocity of the system is
View SolutionA disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
View SolutionA circular disc of mass 0.41 kg and radius 10 m rolls without slipping with a velocity of 2 m/s. The total kinetic energy of disc is
View Solution

