A sphere of radius R has its centre at the origin. It has a uniform mass density ρ0 except that there is a spherical hole of radius r=R/2 whose centre is at x=R/2 as in fig (a) find gravitational field at points on the axis for x>R (ii) Show that the gravitational field inside the hole is uniform, find its magnitude and direction.

The correct Answer is:→g=πGρ0R36[1(x−(R/2))2−8^(2))]ˆi,ˆg=2πxGρ0R3ˆi
From the principle of superposition field may be consider due to a solid sphere of (radius R) positive mass and solid sphere of (Radius R/2) having negative mass.
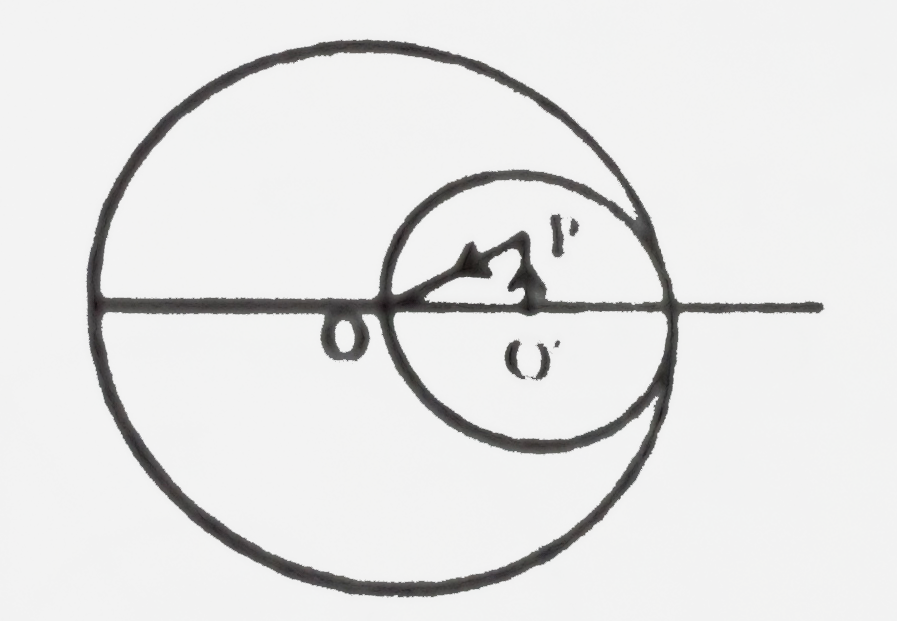
(i)→g=Gρ043πR3x2ˆi+Gρ043π(R/2)3(x−R/2)2
→g=πGρ0R3[−43x2+16(x−R/2)2]ˆi
→g=πGρ0R36[1(x−R/2)2−8x2]ˆi
(ii) →gp =Field due to sphere (R) of positive mass +field due to shpere (R/2) of negative mass
=43πGρ0−−→PO+43πRρ0−−−→O'P
=43πGρ−−→PO+43πRρo−−−→O,P
→gP=43πGρ0−−−→O'O43πGPρ0(−−−→O,P+→PO)
→gp=43πGρ0×R2(−ˆi)
→gP=23πGρ0R(−ˆi)
Similar Questions
A current is passing through a cylindrical conductor with a hole (or cavity) inside it. Show that the magnetic field inside the hole is uniform and find its magnitude and direction.
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View Solution
Knowledge Check
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2A sphere of radius R has a charge density σ. The electric intensity at a point at a distance r from its centre is
AE=σR2∈0kr2BE=σ∈0kCE=R2DE=∈0kr2σ2Mass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
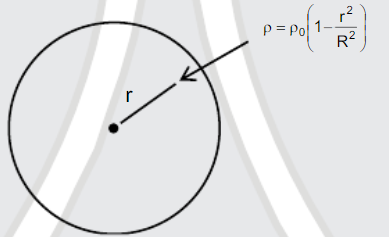 A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A4π3(Gρ0R)B2π√35(Gρ0R)C8π√527(Gρ0R)D2π√527(Gρ0R)
A uniform metal sphere of radius R and mass m is surrounded by a thin uniform spherical shell of same mass and radius 4R. The centre of the shell C falls on the surface of the inner sphere. Find the gravitational fields at points A and B.

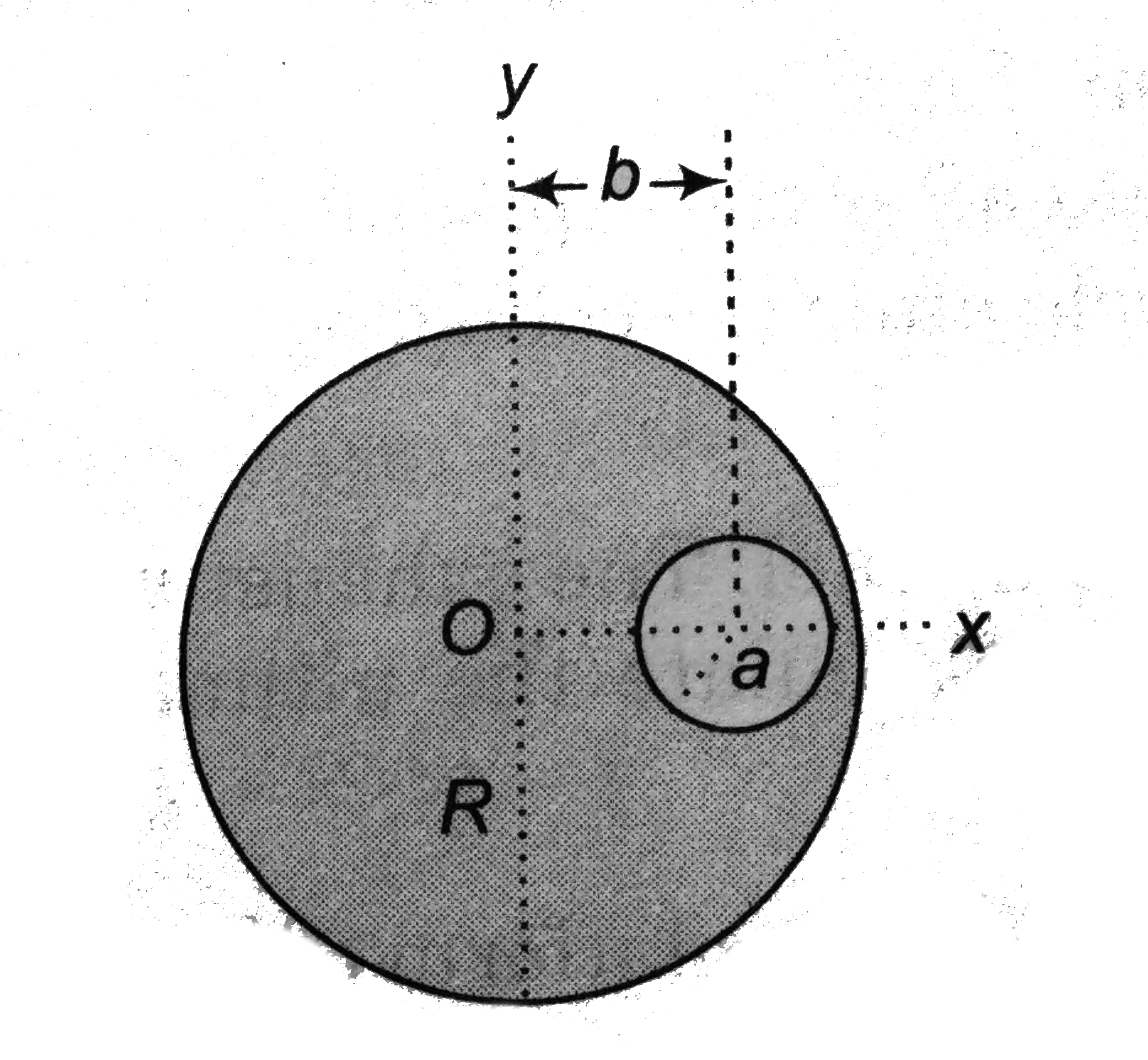
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionThe uniform solid sphere shown in the figure has a spherical hole in it. Find the position of its centre of mass.
View SolutionA sphere of radius 2R has a uniform charge density p. The difference in the electric potential at r = R and r = 0 from the centre is:
View SolutionA spherical cavity is made inside a sphere of density ρ. If its centre lies at a distacne l from the centre of the sphere, show that the gravitational field strength of the field inside the cavatiy is
E=4π3Glρ
View Solution

