A uniform disc of radius R has a hole cut out which has a radius r. The centre of hole is at a distance R2 from the centre of disc. The position of centre of mass is : Solution in Kannada
R−rR
Rr22(R2−r2)
Rr22(R2+r2)
None of these
The correct Answer is:B
Mass of complete disc =πR2tρ
(t = thickness)
Mass of scooped out disc = πr2tρ
Mass of remaining disc = π(R2−r2)tρ
Now π(R2−r2)tρ×x=πr2tρR2x=r2R2(R2−r2)
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - LEVEL-III (MCQ)
10 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - ROTATIONAL MOTIONEXERCISE - RCQ
8 Videos
- RAY OPTICSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICSEXERCISE - RECENT COMPETITIVE QUESTION
32 Videos
- SOLIDS & SEMICONDUCTOR DEVICESBOOK - MODERN PUBLICATIONCHAPTER - SOLIDS & SEMICONDUCTOR DEVICESEXERCISE - Revision Test
28 Videos
Similar Questions
Two particles of equal mass 'm' go around a circle of radius 'R' under the action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is :
View SolutionThe moment of inertia of a circular disc of radius 2 m and mass 1 kg about an axis passing through the centre of mass but perpendicular to the plane of the disc is 2 kg m2. Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is :

View SolutionThe moment of inertia of a circular disc of radius 2 m and mass 1 kg about an axis passing through the centre of mass but perpendicular to the plane of the disc is 2 kg m2. Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is :

View SolutionA point object O is placed in front of a glass rod having spherical end of radius of curvature 30 cm. The image would be formed at

View SolutionChoose the forward biased p-n junction :
View SolutionFigure shows a uniform disc of radius R , from which a hole of radius R/2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
View SolutionA disc (of radius r cm) of uniform thickness and uniform density σ has a square hole with sides of length l=r√2cm. One corner of the hole is located at the centre of the disc and centre of the hole lies y-axis as shown. Then the y-coordinate of position of centre of mass of disc with hole (in cm) is.
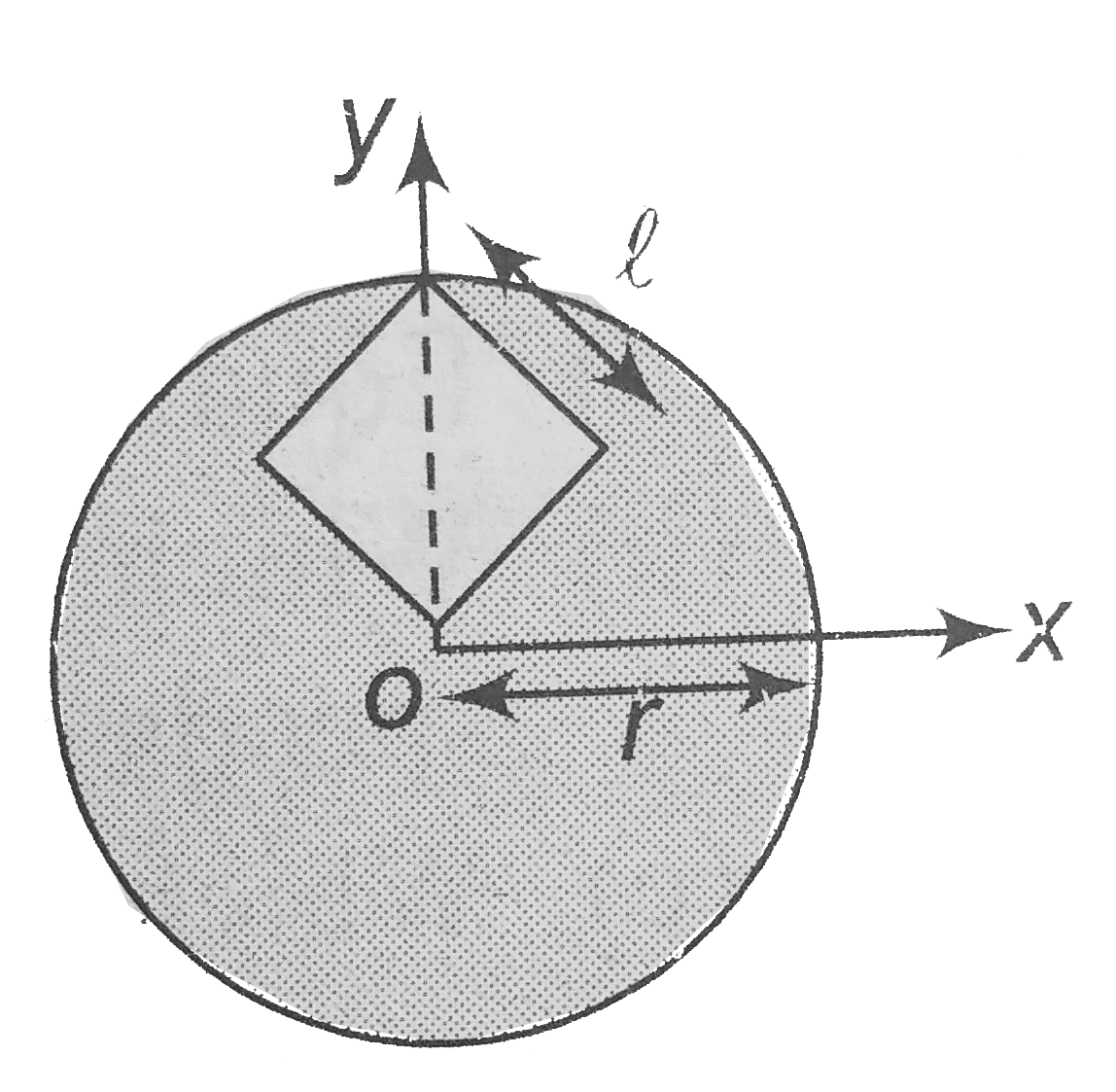 .
.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View SolutionA circular section of radius r si cut out of a uniform disc of radius R, the centre of the hole being R/2 from the centre of the original disc. Locate the centre of gravity of the remainder.
View SolutionFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionFrom a uniform disc of radius R, a circular disc of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of original disc. Locate the centre of gravity of the resultant flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View SolutionFrom a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
View Solution
