A uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
To find the pressure p inside a uniform sphere as a function of the distance r from its center, we will follow these steps:
Step 1: Determine the Density of the Sphere
The density ρ of the sphere can be calculated using the formula:
ρ=M43πR3
where M is the mass of the sphere and R is its radius.
Step 2: Consider a Spherical Shell
Consider a small spherical shell of radius r and thickness dr inside the sphere. The volume dV of this shell is given by:
dV=4πr2dr
Step 3: Calculate the Mass of the Shell
The mass dm of the shell can be expressed as:
dm=ρ⋅dV=ρ⋅4πr2dr
Step 4: Gravitational Force on the Shell
The gravitational force dF acting on this shell due to the mass of the sphere inside it can be calculated using Newton's law of gravitation. The mass of the sphere that contributes to the gravitational force is the mass enclosed within radius r:
dF=G⋅Menc⋅dmr2
where Menc=43πr3ρ.
Step 5: Relate Pressure Change to Gravitational Force
The change in pressure dP due to the gravitational force acting on the shell is given by:
dP=dF4πr2
Substituting dF into this equation gives:
dP=G⋅Menc⋅dm4πr4
Step 6: Substitute for Mass and Density
Substituting Menc and dm into the equation for dP:
dP=G⋅(43πr3ρ)⋅(ρ⋅4πr2dr)4πr4
This simplifies to:
dP=G⋅ρ2⋅4π3⋅r⋅dr
Step 7: Integrate to Find Total Pressure
To find the total pressure P at a distance r from the center, integrate dP from r to R:
P=∫RrdP=∫RrG⋅ρ2⋅4π3⋅rdr
This results in:
P=23G⋅ρ2⋅(R2−r2)
Step 8: Substitute for Density
Substituting the expression for density ρ:
P=23G⋅⎛⎝M43πR3⎞⎠2⋅(R2−r2)
Step 9: Evaluate Pressure at the Center of the Earth
To find the pressure at the center of the Earth (r=0):
P=23G⋅⎛⎜
⎜⎝M2(43πR3)2⎞⎟
⎟⎠⋅R2
Substituting the values for the mass and radius of the Earth (M=5.97×1024 kg and R=6.4×106 m) will yield the pressure at the center.
Final Answer
After substituting the values and calculating, we find that the pressure at the center of the Earth is approximately:
P≈1.72×1011Pa
---
The density ρ of the sphere can be calculated using the formula:
ρ=M43πR3
where M is the mass of the sphere and R is its radius.
Consider a small spherical shell of radius r and thickness dr inside the sphere. The volume dV of this shell is given by:
dV=4πr2dr
The mass dm of the shell can be expressed as:
dm=ρ⋅dV=ρ⋅4πr2dr
The gravitational force dF acting on this shell due to the mass of the sphere inside it can be calculated using Newton's law of gravitation. The mass of the sphere that contributes to the gravitational force is the mass enclosed within radius r:
dF=G⋅Menc⋅dmr2
where Menc=43πr3ρ.
The change in pressure dP due to the gravitational force acting on the shell is given by:
dP=dF4πr2
Substituting dF into this equation gives:
dP=G⋅Menc⋅dm4πr4
Substituting Menc and dm into the equation for dP:
dP=G⋅(43πr3ρ)⋅(ρ⋅4πr2dr)4πr4
This simplifies to:
dP=G⋅ρ2⋅4π3⋅r⋅dr
To find the total pressure P at a distance r from the center, integrate dP from r to R:
P=∫RrdP=∫RrG⋅ρ2⋅4π3⋅rdr
This results in:
P=23G⋅ρ2⋅(R2−r2)
Substituting the expression for density ρ:
P=23G⋅⎛⎝M43πR3⎞⎠2⋅(R2−r2)
To find the pressure at the center of the Earth (r=0):
P=23G⋅⎛⎜
⎜⎝M2(43πR3)2⎞⎟
⎟⎠⋅R2
Substituting the values for the mass and radius of the Earth (M=5.97×1024 kg and R=6.4×106 m) will yield the pressure at the center.
After substituting the values and calculating, we find that the pressure at the center of the Earth is approximately:
P≈1.72×1011Pa
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Calculate the pressure the pressure caused by gravitational compressions inside the earth , at a distance r from its centre . Take M as the mass of the earth of the earth and R as its radius .
View SolutionThere is a uniform sphere of mass M and radius R. Find the strength G and the potential varϕ of the gravitational field of this sphere as a function of the distance r from its centre (with r<R and r>R). Draw the approximate plots of the functions G(r) and φ(r).
View Solution
Knowledge Check
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
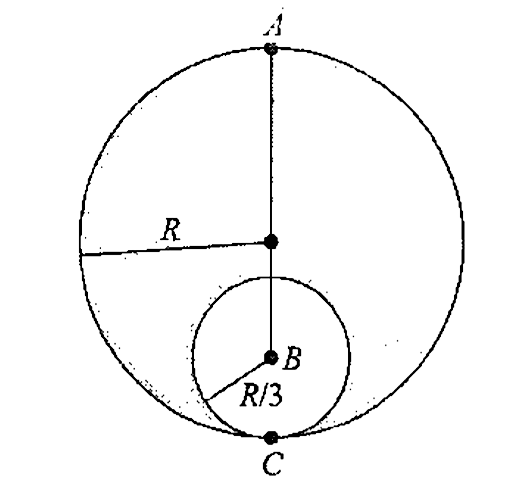 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GmrC−GM2rD−4GMrTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
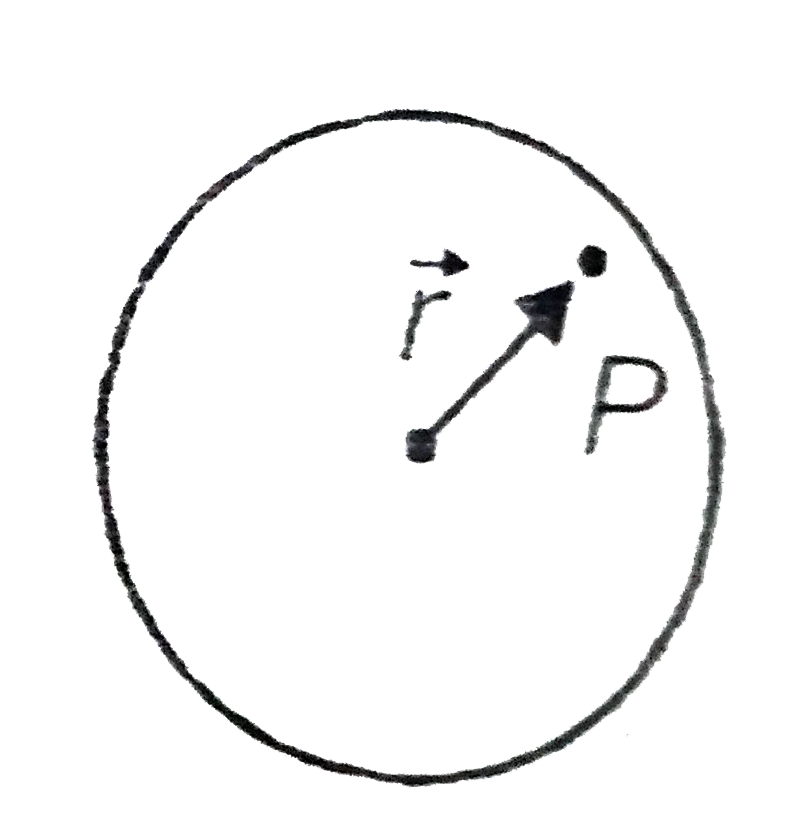
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution

