On the pole of the Earth a body is imparted velocity v0 directed vertically up. Knowing the radius of the Earth and the free-fall acceleration on its surface, find the height to which the body will ascend. The air drag is to be neglected.
Let the mass of the body be m and let it go upto a height h.
From conservation of mechanical energy of the system
−γMmR+12mv20=−γMm(R+h)=0
Using γMR2=g, in above equation and on solving we get,
h=Rv202gR−v20
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Elastic Deformation Of Asolid Body
Explore 25 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Laws Of Conservation Of Energy, Momentum And Angular Momentum
Explore 82 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A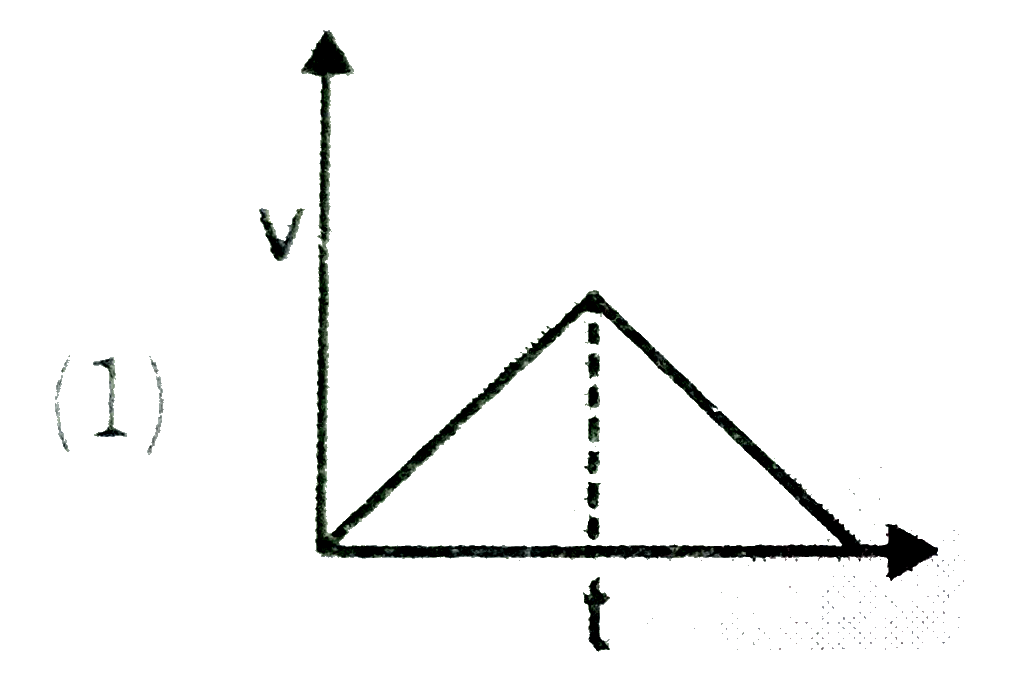 B
B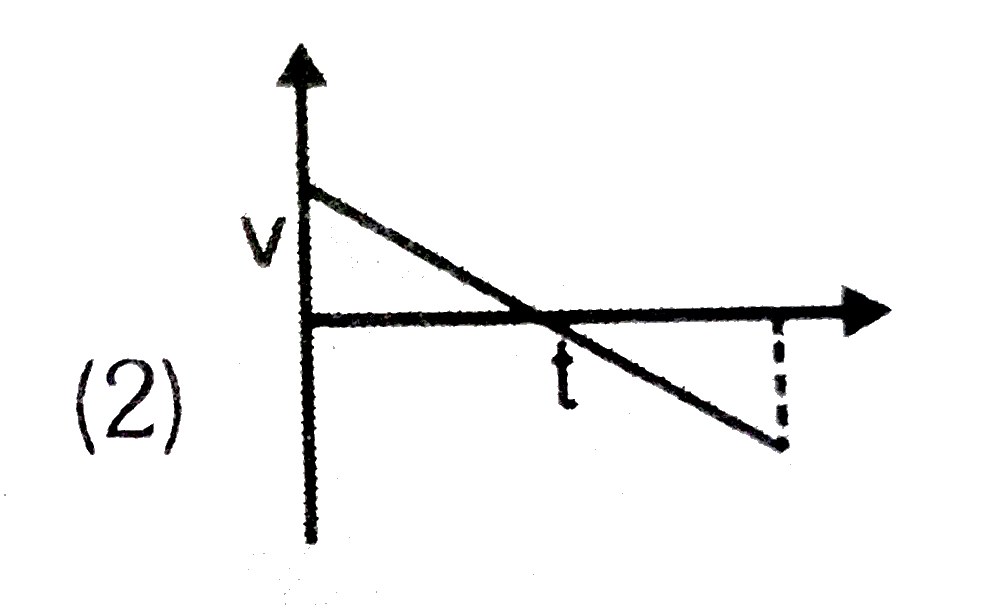 C
C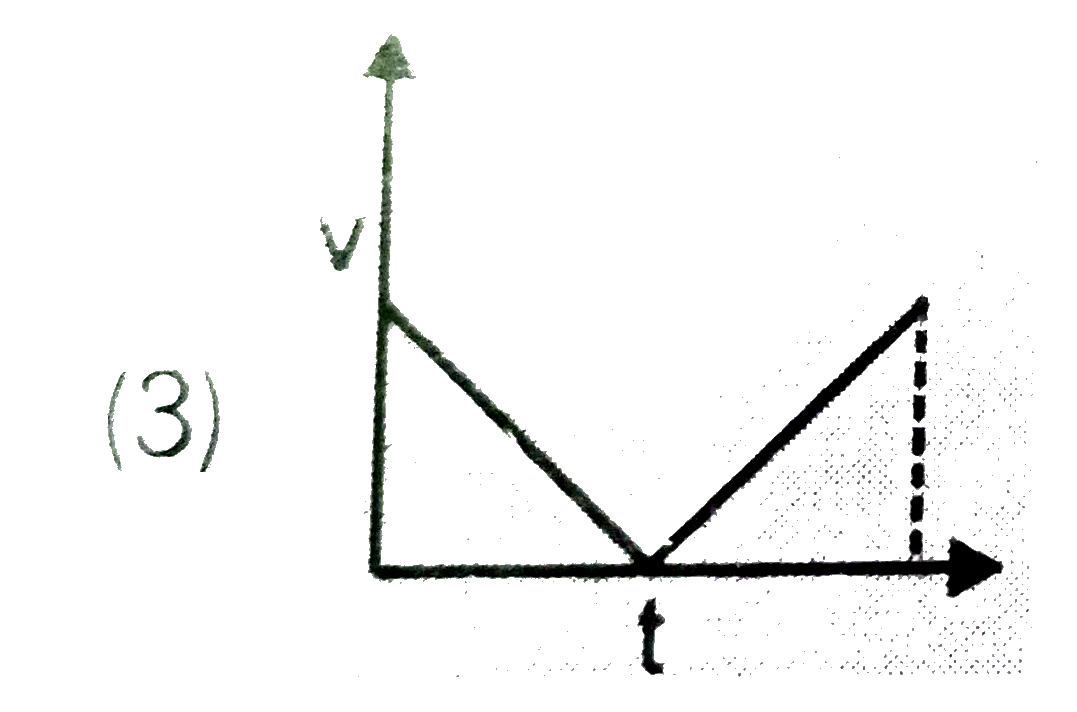 D
D
A particle is projected vertically upwards with a velocity √gR, where R denotes the radius of the earth and g the acceleration due to gravity on the surface of the earth. Then the maximum height ascended by the particle is
AR2BRC2RD5R4A body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
A1:1B1:2C1:3D1:4
A body of mass m is from surface of the earth projected vertically upwards with a velocity such that it rises to a height of 20 m. If the same body is projected with same velocity from a planet density is 14 th of density of earth and radius is 12 of that of Earth, then find the height to which the body will rise on the planet.
View SolutionAn artificial satellite is launched into a circular orbit around the Earth with velocity v relative to the reference frame moving translationally and fixed to the Earth's rotation axis. Find the distance from the satellite to the Earth's surface. The radius of the Earth and the free-fall acceleration on its surface are supposed to be known.
View SolutionA body projected from the surface of the earth attains a height equal to the radius of the earth. The velocity with which the body was projected is
View SolutionAs it falls, the acceleration of a body dropped from the height equal to that of radius of earth,
View SolutionA projectile is fired vertically upwards from the surface of the earth with a velocity Kve, where ve is the escape velocity and K<1.If R is the radius of the earth, the maximum height to which it will rise measured from the centre of the earth will be (neglect air resistance)
View Solution

