A uniform solid of valume mass density $ρ$ and radius R is shown in figure.

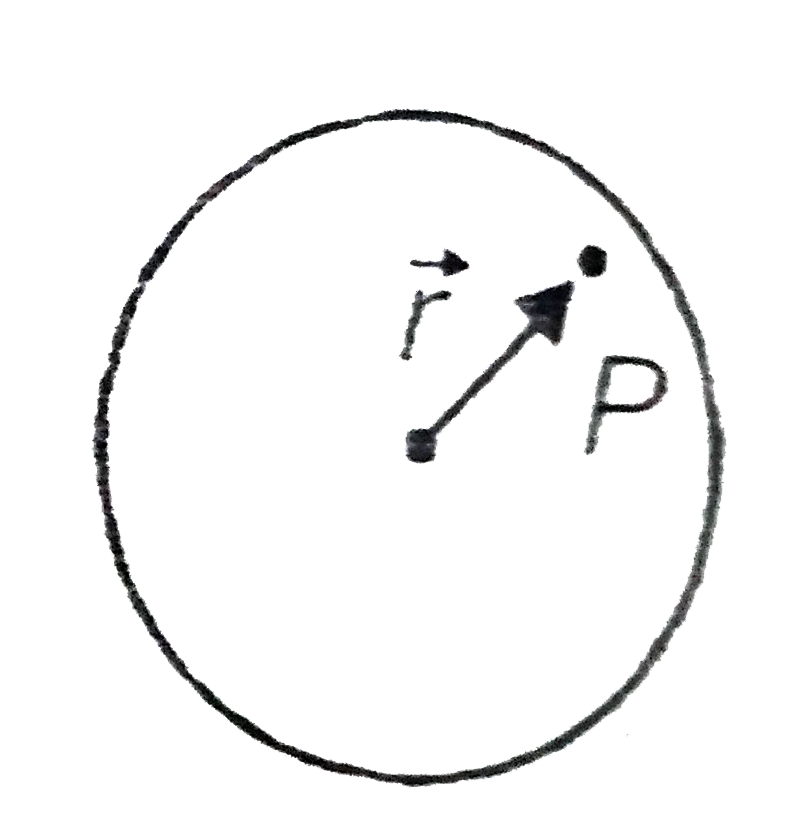
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector $\to l$ in terms of radius vector $\to r$ of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field $\to E$ at point P in vector formulationand interpret the result.

Video Solution

Text Solution

Verified by Experts

(a) $\frac{4 π G ρ r}{3}, - \frac{4}{3} π G ρ \to r$
(b) $- \frac{4}{3} π G ρ \to a$ , where $\to a$ is position vector of centre of cavity w.r.t. centre of solid sphere.

Updated on:21/07/2023

The gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
A $\frac{G M}{a^{2}}$
B $\frac{G M}{a^{3}}$
C $\frac{G M}{2 a}$
Dzero
Inside a uniform sphere of density $ρ$ there is a spherical cavity whose centre is at a distance $l$ from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
A $E = \frac{- 2}{3} π G ρ l$
B $E = \frac{- 4}{3} π G ρ l$
C $E = \frac{- 4}{3} π^{2} G ρ l$
D $E = \frac{- 4}{3} π G ρ^{2} l^{2}$
Let $ρ (r) = \frac{Q r}{π R^{4}}$ be the charge density distribution for a solid sphere of radius R and total charge Q. For a point P inside the sphere at a distance $r_{1}$ from the centre of the sphere, the magnitude of electric field is
A $\frac{Q}{4 π ε_{0} r_{1}^{2}}$
B $\frac{Q r_{1}^{2}}{4 π ε_{0} R^{4}}$
C $\frac{Q r_{1}^{2}}{3 π ε_{0} R^{4}}$
Dzero