Gravitational field at the surface of a solid sphere is 1.5×10−4N kg−1. Find the gravitational field at a point situated inside the sphere at a distance equal to half of rhe radius of the solid sphere.
7.5×10−4N kg−1
7.5×104N kg−1
70.5×10−4N kg−1
=1.5×10−7N kg−1
The correct Answer is:A
Let mass of the solid sphere is M and radius is R Its is given that
Esurface=GMR2=1.5×10−4
∴E(r=R/2)=GMR3(R/2)
=GM2R2=1.5×10−42
=7.5×10−4N kg−1.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Solved Examples
16 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
Find total surface area of a solid hemi-sphere of radius 7cm.
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
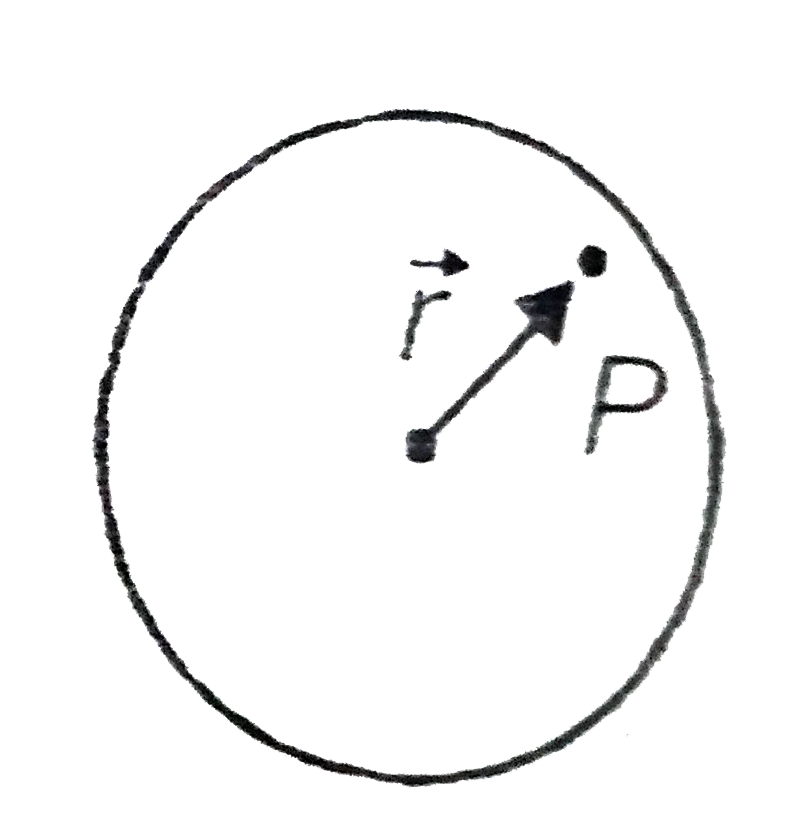
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View Solution
Knowledge Check
Gravitational field due to a solid sphere
Aremains constant throughout the sphereBincrease inside the sphere and decreases outside the sphereCincreases throughout with distance from the centerDdecreases throughout with distance from the centreThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
AGMa2BGMa3CGM2aDzero
Statement I: The magnitude of the gravitational potential at the surface of solid sphere is less than that of the centre of sphere. Statement II: Due to the solid sphere, the gravitational potential is the same within the sphere.AStatement I is True, Statement II is True: Statement II is a correct explanation for Statement I.BStatement I is True, Statement II is True: Statement II is Not a correct explanation for Statement I.CStatement I is True, Statement II is False.DStatement I is False, Statement II is True.
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionThe gravitational field intensity at a point 10 × 103 km from the centre of the earth is 4.8 N kg−1 . The gravitational potential at that point is
View SolutionThe gravitational force on a body of mass 1.5 kg situated at a point is 45 M . The gravitational field intensity at that point is .
View SolutionThe charge density on the surface of a conducting sphere is 64×10−7C/m2 and the electric intensity at a distance of 2 m from the centre of the sphere is 4π×104N/C. The radius of the sphere is
View SolutionThe charges given to a hollow sphere of radius 10 cm is 10 n C . Electric field at a point situated at a distance of 4 cm from its centre is
View Solution