A block of mass M attached to the free end of a spring of force constant k is nounted on a smooth horizontal table as shown in figure.
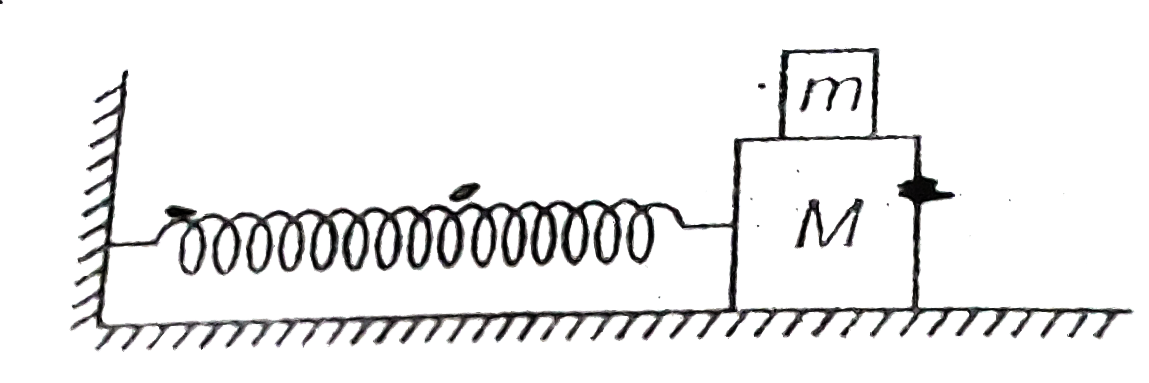
The block executes SHM with amplitude A and frequency f . If an object of mass m is put on it, when the block is passing through its equilibium position and the two move together ,then what is the new amplitude and frequency of vibration?
Initially the mass of osciallting system is M
∴f=12π√kM
Let f be the new frequency and A' be the new amplitude of vibration.
When block of mass m block M, then the total mass of osciallting system becomes M+m
∵f'=12π√k(m+M)
Now l'f=√M(m+M)
∴f'=f√M(m+M) .....(i)
The new frequency of oscillaiton f' is less than f
When mass M passes through its mean position, it has maximum speed.
Let v and V be the speed of block of mass M and M+mrespectively at equilibrium position.
By conservation of linear momentum for the collision.
Mv=(m+M)V
But at equilibrium position
v=Aω=A×2πf
∴Ma(2πf)=(m+M)A'2πf
⇒A'A=M(m+M)×ff'
Using equation (i), we have
A'=A√M(m+M)
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
A horizontal spring block system of mass M executes simple har monic motion.w hen the block is passingle through its equilibrium position, an object of mass m is put on it and the two move tother. Find the new amplitude and frequency of vibration.
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View Solution
Knowledge Check
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4A horizontal spring-block system of mass 1kg executes SHM of amplitude 10 cm. When the block is passing through its equilibrium position another mass of 1kg is put on it and the two move together.
Aamplitude will remain unchangedBamplitude will become 5√2 cmCthe frequency of oscillations will remain sameDthe frequency of oscillations will decrease.A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvk
A horizontal spring block system of mass M executes simple haormonic motion. When the block is passing through its equilibrium position, an object of mass m is put on it and the two move together. Find the new amplitude and frequency of vibration. Given, k is the spring constant of the system.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass M is lying on a frictionless horizontal surface and it connected to a spring of spring constant k, whose other end is fixed to a wall, system executes simple harmonic motion of amplitude A0, when the block is passing through its equilibrium positions, an object of mass m is put on it and the two move together with a new time period T and amplitude A. Find the value of T and A in terms of given constants.
View SolutionA block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA horizontal spring -block system of mass 2kg executes S.H.M when the block is passing through its equilibrium positiojn an object of mass 1kg is put on it the two move togather The new amplitude of vibration is (A being its initial amplitude)
View Solution
