Find magnetic field at centre of hexagon wire of side a system carrying current 'I' at centre with 50 turn in multiple of μ0Iaπ
500√3
50√3
50
100
The correct Answer is:A
To find the magnetic field at the center of a hexagonal wire carrying current I with 50 turns, we will follow these steps:
Step 1: Understanding the Geometry of the Hexagon
We start by visualizing a regular hexagon with each side of length a. The center of the hexagon is equidistant from all its vertices.
Step 2: Finding the Distance from the Center to a Side
The distance R from the center of the hexagon to the midpoint of one of its sides can be derived using trigonometry. For a regular hexagon:
- The angle subtended at the center by each side is 60∘.
- The half-angle is 30∘.
- The height from the center to the midpoint of a side can be calculated as:
R=a2tan(30∘)=a2⋅1√3=a√32
Step 3: Magnetic Field Due to One Side of the Hexagon
The magnetic field B at the center due to a straight wire carrying current I is given by the formula:
B=μ0I4πR⋅(sinθ1+sinθ2)
where θ1 and θ2 are the angles from the wire to the point where the field is being calculated. For our case:
- θ1=θ2=30∘
- Thus, sin(30∘)=12
Substituting these values, we get:
Bone side=μ0I4π⋅a√32⋅(12+12)=μ0I4π⋅a√32⋅1=μ0I2πa√3
Step 4: Total Magnetic Field Due to All Sides
Since the hexagon has 6 sides, the total magnetic field Btotal at the center due to all sides is:
Btotal=6⋅Bone side=6⋅μ0I2πa√3=3μ0Iπa√3
Step 5: Considering the Number of Turns
Given that there are 50 turns, the total magnetic field at the center due to all turns is:
Bnet=50⋅Btotal=50⋅3μ0Iπa√3=150μ0Iπa√3
Step 6: Expressing in Required Form
To express this in terms of μ0Iπa:
Bnet=150μ0Iπa√3=150√3⋅μ0Iπa
Calculating 150√3:
150√3=50√3
Thus, the final answer for the magnetic field at the center of the hexagon wire is:
Bnet=50√3⋅μ0Iπa
Final Answer
The magnetic field at the center of the hexagon wire is 50√3⋅μ0Iπa.
---
We start by visualizing a regular hexagon with each side of length a. The center of the hexagon is equidistant from all its vertices.
The distance R from the center of the hexagon to the midpoint of one of its sides can be derived using trigonometry. For a regular hexagon:
- The angle subtended at the center by each side is 60∘.
- The half-angle is 30∘.
- The height from the center to the midpoint of a side can be calculated as:
R=a2tan(30∘)=a2⋅1√3=a√32
The magnetic field B at the center due to a straight wire carrying current I is given by the formula:
B=μ0I4πR⋅(sinθ1+sinθ2)
where θ1 and θ2 are the angles from the wire to the point where the field is being calculated. For our case:
- θ1=θ2=30∘
- Thus, sin(30∘)=12
Bone side=μ0I4π⋅a√32⋅(12+12)=μ0I4π⋅a√32⋅1=μ0I2πa√3
Since the hexagon has 6 sides, the total magnetic field Btotal at the center due to all sides is:
Btotal=6⋅Bone side=6⋅μ0I2πa√3=3μ0Iπa√3
Given that there are 50 turns, the total magnetic field at the center due to all turns is:
Bnet=50⋅Btotal=50⋅3μ0Iπa√3=150μ0Iπa√3
To express this in terms of μ0Iπa:
Bnet=150μ0Iπa√3=150√3⋅μ0Iπa
Calculating 150√3:
150√3=50√3
Bnet=50√3⋅μ0Iπa
The magnetic field at the center of the hexagon wire is 50√3⋅μ0Iπa.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The magnetic field at centre of a hexagonal coil of side l carrying a current I is
 A√3μ0IπlBμ0I4πlCπμ0I√3lDzero
A√3μ0IπlBμ0I4πlCπμ0I√3lDzeroMagnetic field induction at the centre of a square loop of side 'a' carrying current I as shown in figure is
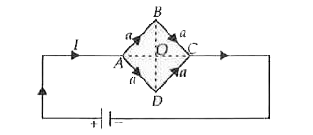 Aμ0I√2πaB2μ0IπaCμ0I2πaDzero
Aμ0I√2πaB2μ0IπaCμ0I2πaDzeroThe magnetic field at the centre of current carrying coil is
Aμ0ni2rBμ02πnirCμ0ni4rDμ0ni
Magnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionFind the magnetic field B due to a semicircular wire of radius 10.0 cm carrying a current of 5.0A at its centre of curvature .
View SolutionThe magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
View Solution