The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
9μ0i4πL
3√3μ0i4πL
2√3μ0iπL
3μ0i4πL
The correct Answer is:A
To find the magnetic field at the center of an equilateral triangular loop of side 2L carrying a current I, we can follow these steps:
1. Understand the Geometry of the Triangle:
- We have an equilateral triangle with each side measuring 2L.
- The center of the triangle is equidistant from all three sides.
2. Determine the Angle at the Center:
- In an equilateral triangle, the angle at each vertex is 60 degrees.
- Therefore, the angle subtended at the center by each side of the triangle is 120 degrees (360 degrees / 3 sides).
3. Calculate the Magnetic Field Due to One Side:
- The formula for the magnetic field due to a straight current-carrying wire of finite length at a perpendicular distance R is given by:
B=μ0I4πRsinθ
- Here, θ is the angle between the line from the wire to the point where the field is being calculated and the wire itself.
4. Find the Perpendicular Distance (R):
- For an equilateral triangle, the distance from the center to a side can be determined using trigonometry.
- The perpendicular distance R from the center to the midpoint of one side can be calculated as:
R=L√3
- This is derived from the properties of the triangle and the relationship between the sides and angles.
5. Calculate the Magnetic Field for One Side:
- Using the formula for the magnetic field and substituting R and θ:
Bone side=μ0I4π(L√3)sin(60∘)
- Since sin(60∘)=√32:
Bone side=μ0I4π(L√3)⋅√32
6. Simplify the Expression:
- Simplifying gives:
Bone side=μ0I√38πL
7. Calculate the Total Magnetic Field:
- Since there are three sides contributing equally to the magnetic field at the center:
Btotal=3×Bone side=3×μ0I√38πL
- This simplifies to:
Btotal=3μ0I√38πL
8. Final Expression:
- The final expression for the magnetic field at the center of the equilateral triangle loop is:
B=9μ0I4πL
- We have an equilateral triangle with each side measuring 2L.
- The center of the triangle is equidistant from all three sides.
- In an equilateral triangle, the angle at each vertex is 60 degrees.
- Therefore, the angle subtended at the center by each side of the triangle is 120 degrees (360 degrees / 3 sides).
- The formula for the magnetic field due to a straight current-carrying wire of finite length at a perpendicular distance R is given by:
B=μ0I4πRsinθ
- Here, θ is the angle between the line from the wire to the point where the field is being calculated and the wire itself.
- For an equilateral triangle, the distance from the center to a side can be determined using trigonometry.
- The perpendicular distance R from the center to the midpoint of one side can be calculated as:
R=L√3
- This is derived from the properties of the triangle and the relationship between the sides and angles.
- Using the formula for the magnetic field and substituting R and θ:
Bone side=μ0I4π(L√3)sin(60∘)
- Since sin(60∘)=√32:
Bone side=μ0I4π(L√3)⋅√32
- Simplifying gives:
Bone side=μ0I√38πL
- Since there are three sides contributing equally to the magnetic field at the center:
Btotal=3×Bone side=3×μ0I√38πL
- This simplifies to:
Btotal=3μ0I√38πL
- The final expression for the magnetic field at the center of the equilateral triangle loop is:
B=9μ0I4πL
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
The magnitude of the magnetic field at the center of an equilateral triangular loop of side 1 m which is carrying a current of 10 A (in μT) is ___________ .
[Take μ0=4π×10−7NA−2]
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View Solution
Knowledge Check
Find the magnitude of the magnetic field at the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
A18μTB1μTC9μTD3μTFind the magnitude of the magnetic field at the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
A18μTB1μTC9μTD3μTThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπL
Magnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
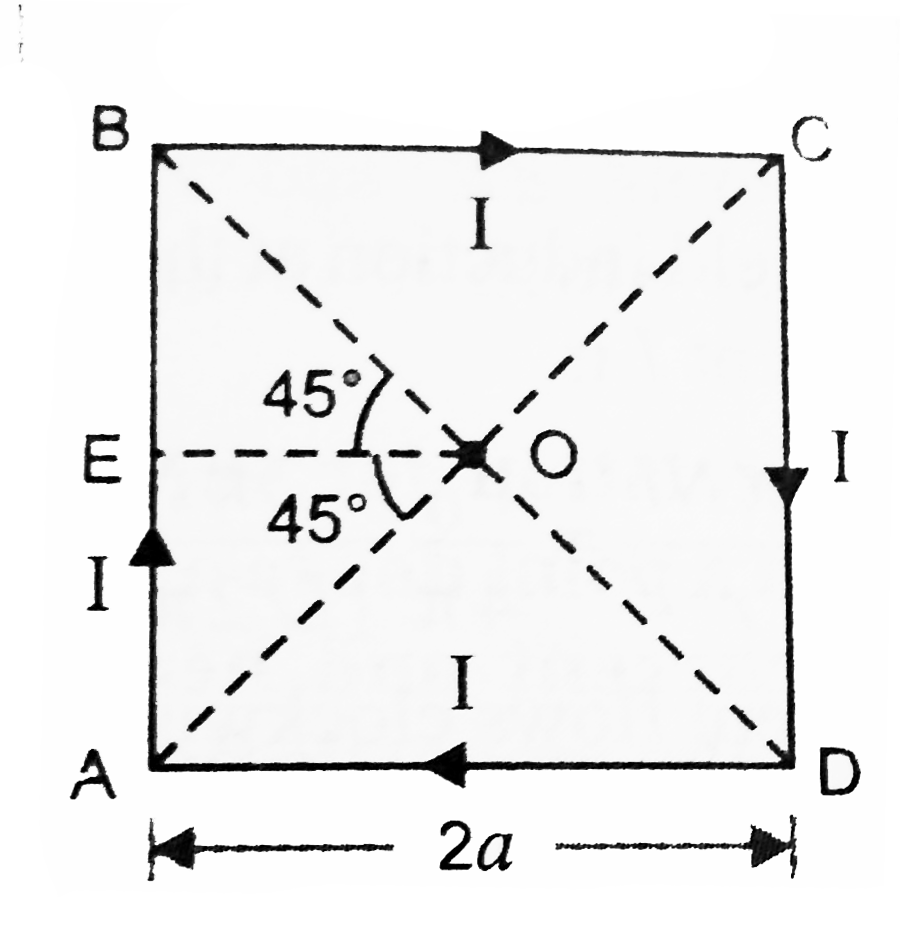
View SolutionFind the experssion for the magnetic field at the centre O of a coil bent in the form of a square of side 2a, carrying current I, figure.
View SolutionThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is measured, Let the measured value be Nμ0IπL. What will be the value of N ?
View SolutionThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
View SolutionMagnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
View Solution
