Two infinite long wires, each carrying current I, are lying along x- and y-axis, respectively. A charged particle, having a charge q and mass m, is projected with a velocity u along the straight line OP. The path of the particle is (neglect gravity)

Straight line
circle
helix
cycloid
The correct Answer is:A
(a) B at all the point lying on OP is zero so u will not be affected
by the magnetic force. Hence, it moves on a straight line.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
An infinitely large plate of surface charge density +σ lying in horizontal xy plane. A particle having charge −q0 and mass m is projected from the plate with velocity u making an angle θ with sheet. Find :
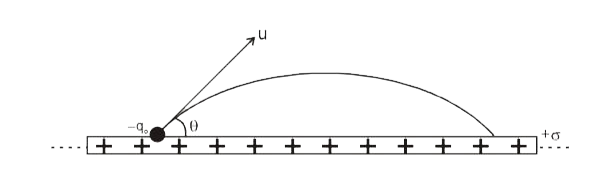
(i) the time taken by the particle to return on the plate.
(ii) maximum height achieved by the particle.
(iii) At what distance will it strike the plate (Neglect gravitational force on the particle)
View SolutionAn infinitely large plate of surface charge density +σ is lying in horizontal xy-plane. A particle having charge −q0 and mass m is projected from the plate with velocity u making an angle θ with sheet. Find :

(i) The time taken by the particle to return on the plate.
(ii) Maximum height achieved by the particle.
(iii) At what distance will it strike the plate (Neglect gravitational force on the particle)
View Solution
Knowledge Check
two infinite wires, carrying currents i1andi2., are lying along x-and y-axes, as shown in the x-y plane. Then,
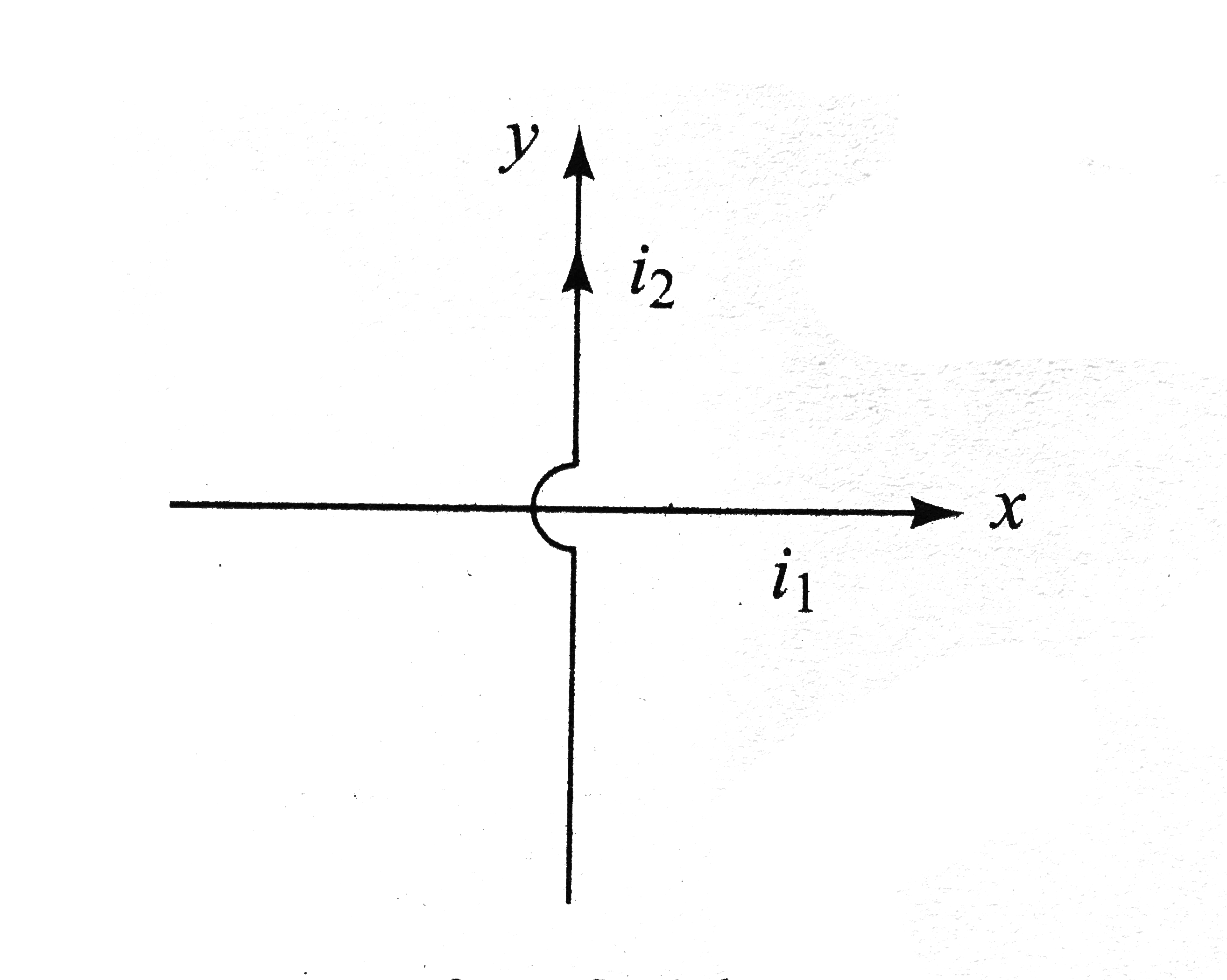 Alocus of points where B is zero is a circleBlocus of points where B is zero is a lineCB decay heperbolically along any line parallel to x-axisDB decay heperbolically along any line parallel to y-axis
Alocus of points where B is zero is a circleBlocus of points where B is zero is a lineCB decay heperbolically along any line parallel to x-axisDB decay heperbolically along any line parallel to y-axisA charged particle of charge q and mass m enters a magnetic field as shown. Find radius of the circular path and the time spent inside the field. Neglect gravity.
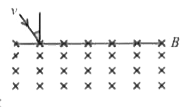 ARπθvBR(π−2θ)vCR(π+2θv)D2Rθv
ARπθvBR(π−2θ)vCR(π+2θv)D2RθvTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Two equal positive charges , Q , are fixed at points (0,d) and (0,−d) on the y-axis. A charged particle having charge −q and mass m is released from rest at point (d,0) on the x-axis . Discuss the motion of charged particle.
View SolutionTwo long straight currents carrying wires having currents I and 2I lie along y-and z-axis, respectively, as shown in Fig. Find →B at a point P(x,0).

View Solution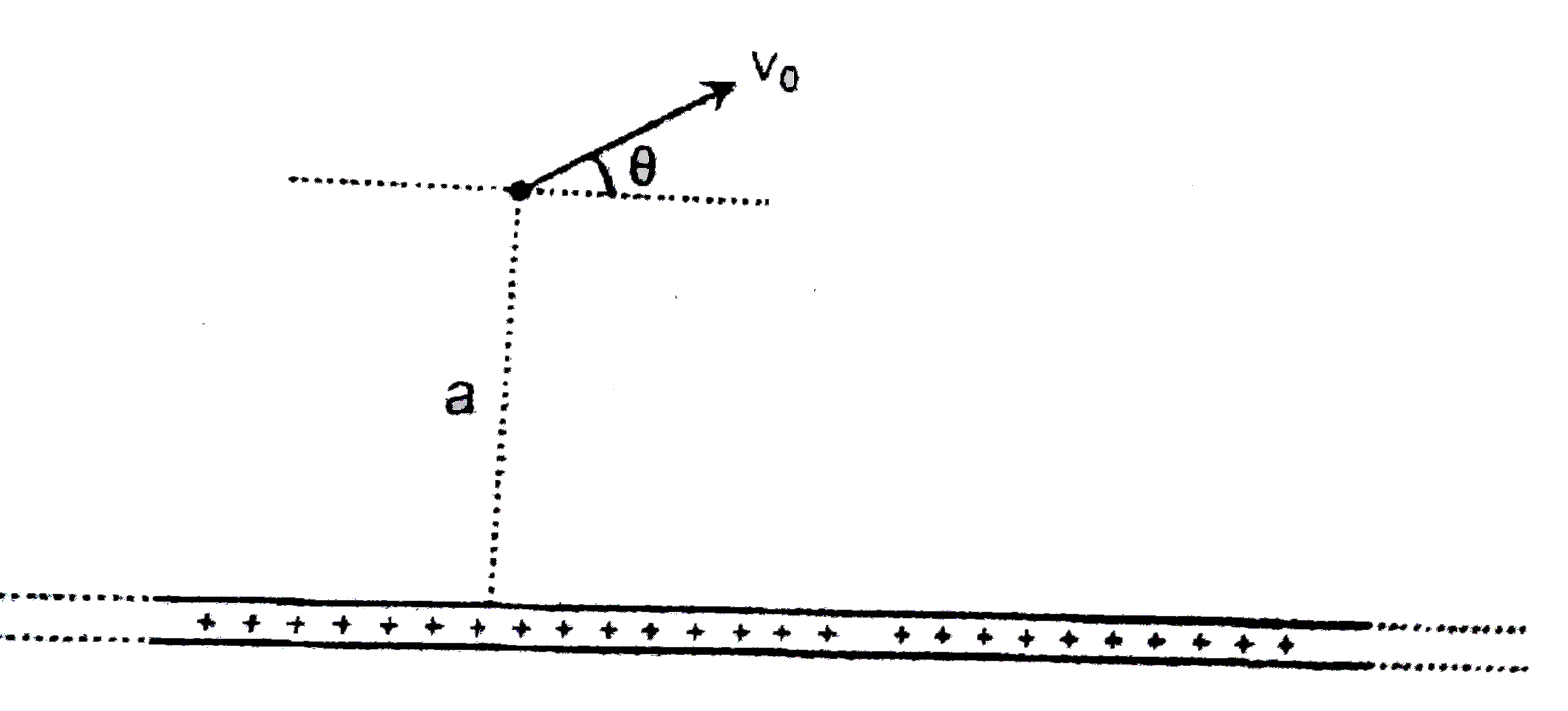
There is an infinite line of uniform linear density of charge +λ. A particle of charge −q & mass m is projected with initial velocity v0 at an angle θ with the line of charge from a distance a from it. The point charge moves in plane containing line charge and point of projection The speed of the particle of found to be minimum when it's distance from the line of charge is ae(nπmε200/qλ). The value of n is (ingnore gravity)
View Solution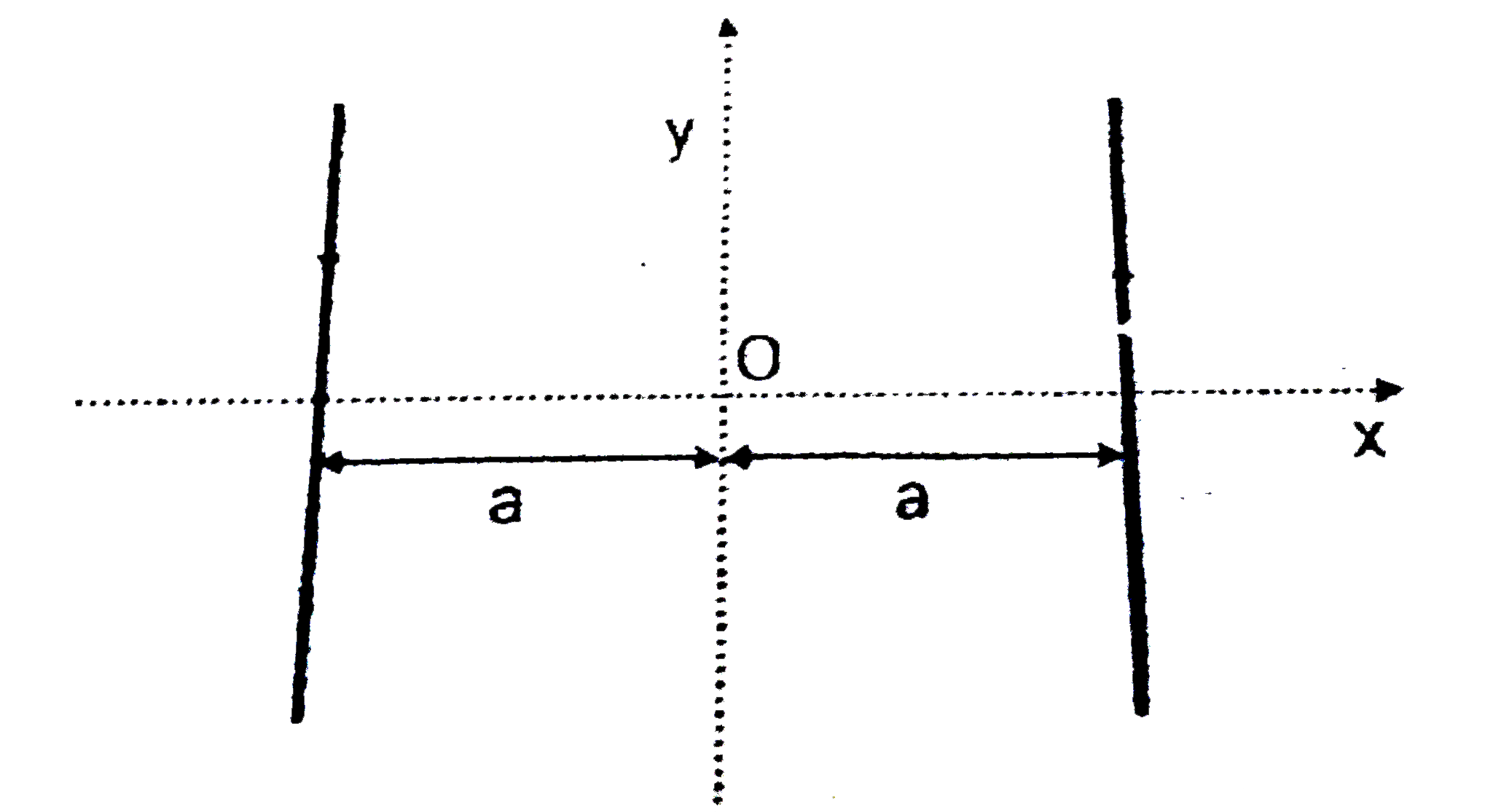
Two infinite long straight current carrying wires are placed parallel to y-axis in x-y plane. Each wire carries current I in opposite direction as shown. A charged particle of charge +q and mass m is projected from position P (0,0,a) with initial velocity →v=→ˆj. Then
View SolutionConsider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be in
View Solution
