A very long straight conducting wire, lying along the z-axis, carries a current of 2A. The integral ∮→B.d→l is computed along the straight line PQ, where P has the coordinates (2cm,2cm,0) and Q has the coordinates (2cm,2cm,0). The integral has the magnitude (in SI units)
π2×10−7
8π×10−7
2π×10−7
π×10−7
The correct Answer is:D
(a) ∫PAQ→B.d→l=∫RBQ→B.d→l(∵∫PCR→B.d→l=0)
(μ0I2πR)(π4R)
=(4π×10−7)(2)16=π×10−72S.I.units
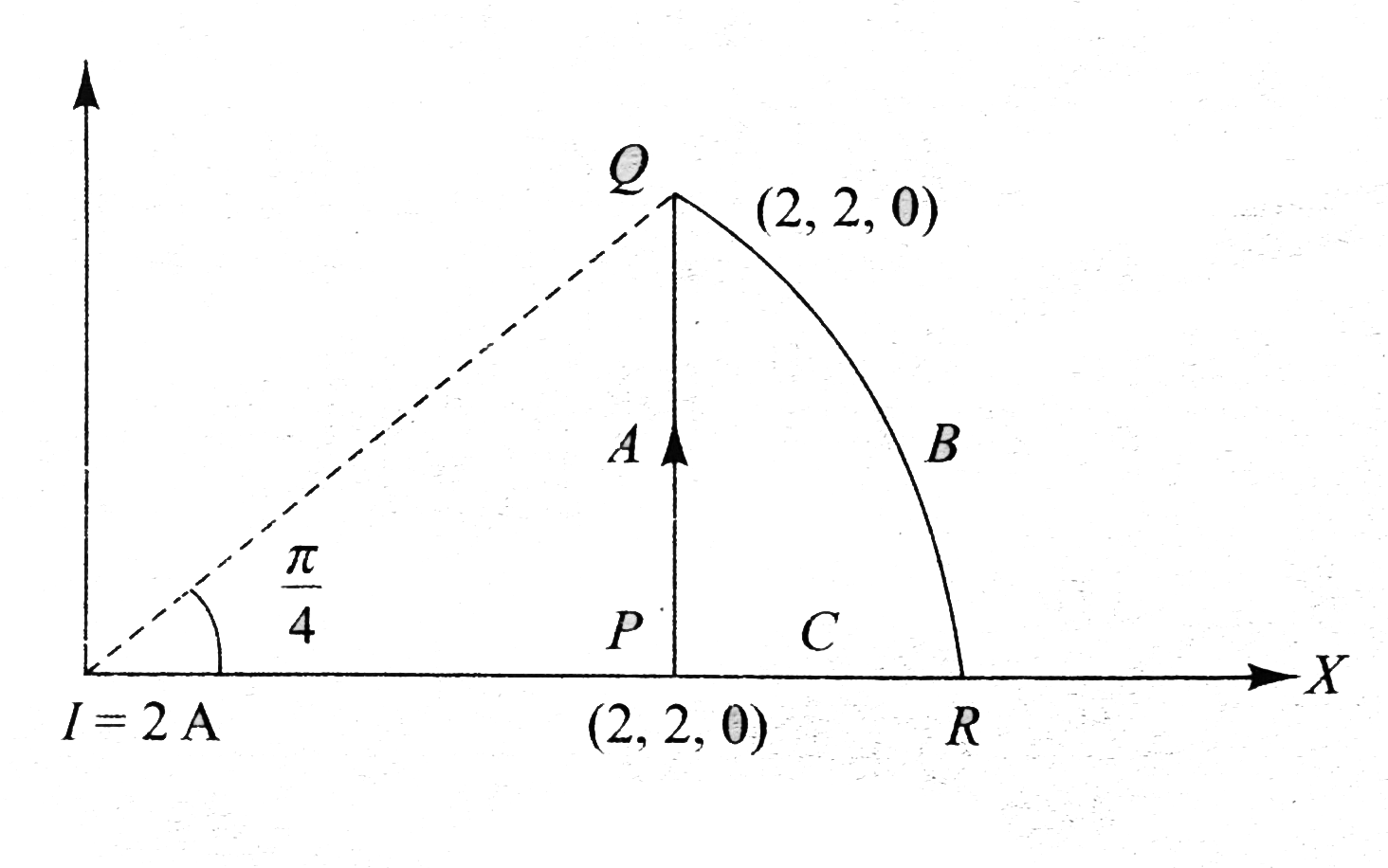
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (multiple Currect )
5 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
KM is a straight line of 13 units If K has the coordinates (2,5) and M has the coordinates (x,−7), find the possible values of x
View SolutionA long conducting wire of radius 1 cm carrying current of 1 A placed with its axis coinciding with X-axis. Find the magnetic field at point having coordinates (0.5cm,0.5cm) .
View Solution
Knowledge Check
A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)A long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)
A very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity →V, as shown, the force on the charge is
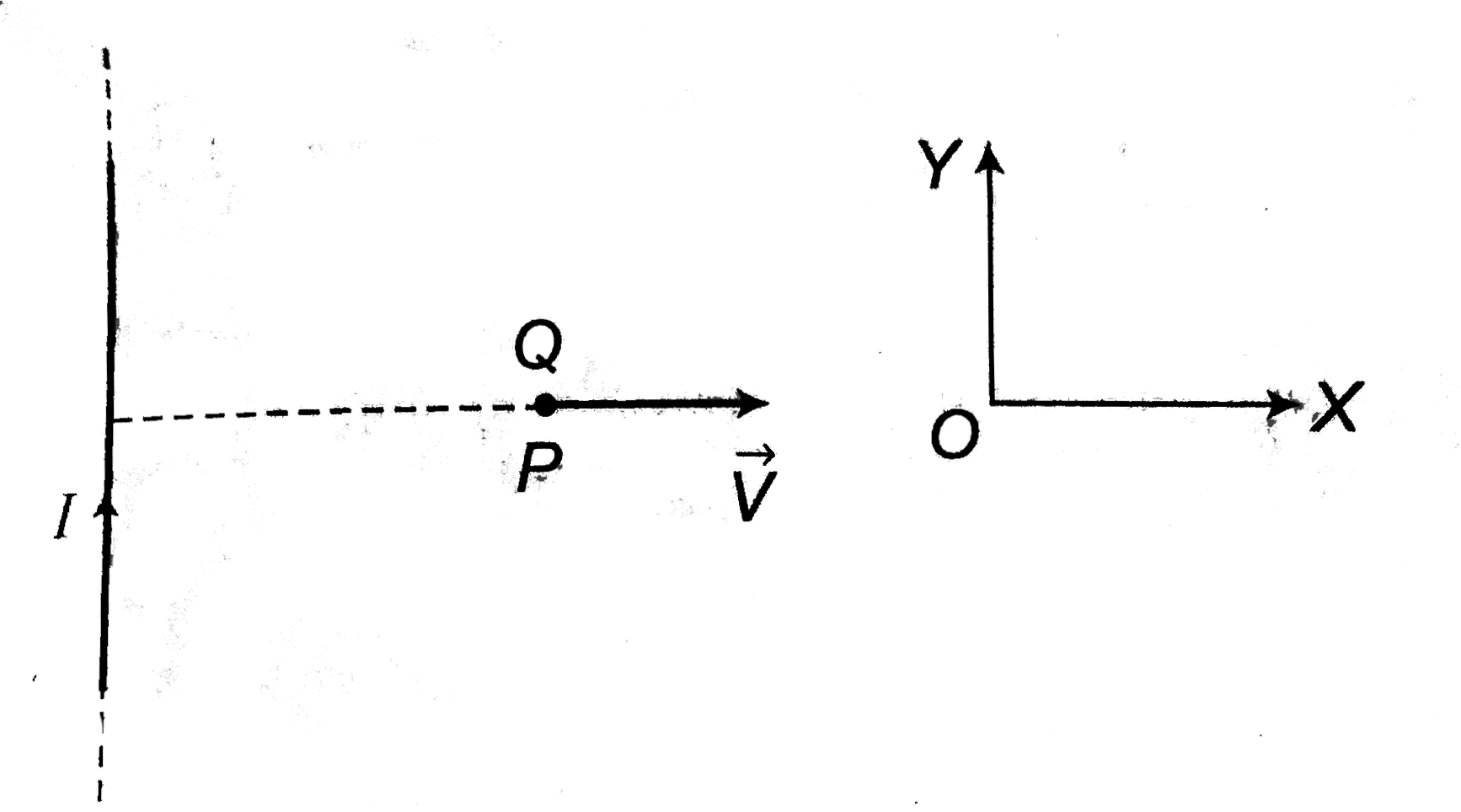
View SolutionA long straight cable contains 7 strands of wire each carrying a current of 5 A. The magnetic induction at a distance of 2 cm from the axis of the cable is
View SolutionA long solenoid has 200 turns per cm and carries a current of 2.5A. The magnetic field at its centre is
View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
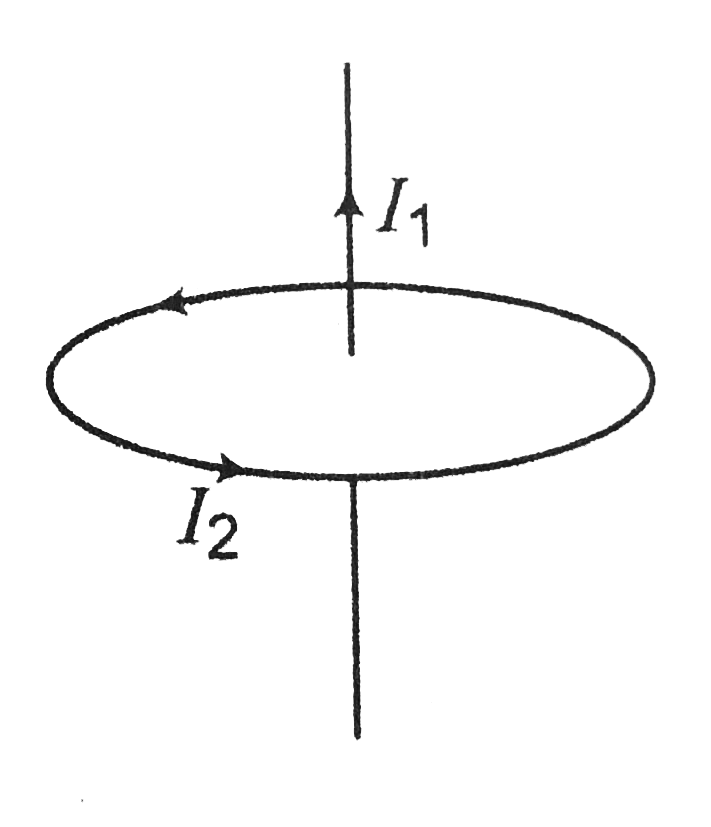
View SolutionThe figure shows a long straight wire carrying a current I1 along the axis of a circular ring carrying a current I_2. Identify the correct statement.
View Solution