An infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is

μ0I4πa(1+b√a2+b2)
μ0I4πa(1−b√a2+b2)
μ0I4πa(b√a2+b2)
none of these
The correct Answer is:B
(b) B=μ0I4πia[sin90+(sin(−θ))]=μ04πia(1−sinθ)
=μ04πia(1−b√a2+b2)

Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (multiple Currect )
Explore 5 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (assertion-reasioning )
Explore 2 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICSChapter:SOURCES OF MAGNETIC FIELDExercise:Exercise (subjective )
Explore 10 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:CENGAGE PHYSICSChapter:SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:QUESTION BANK
Explore 12 Videos
- THERMAL PROPERTIES OF MATTERBook:CENGAGE PHYSICSChapter:THERMAL PROPERTIES OF MATTERExercise:Question Bank
Explore 40 Videos
Similar Questions
A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionThere are two infinite long parallel straight current carrying wires, A and B separated by a distance r. Figure. The current in each wire is I. The ratio of magnitude of magnetic field at point P and Q when points P and Q lie in the plane of wires is:
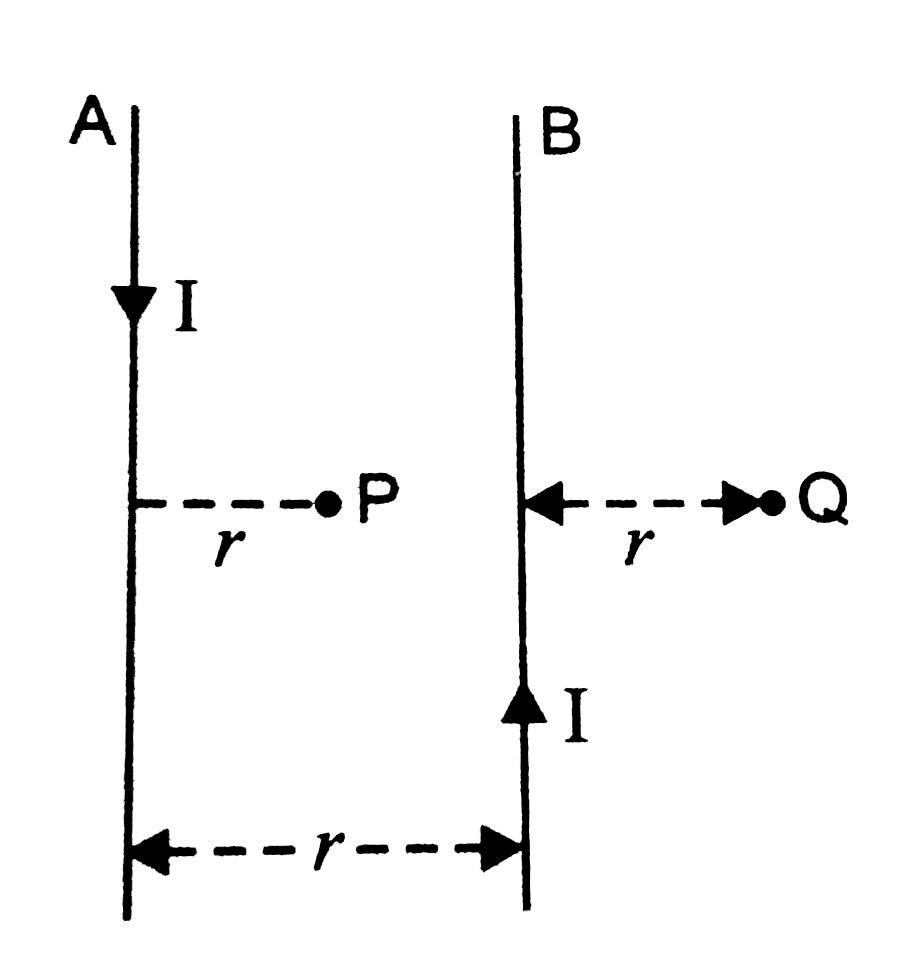
View Solution
Knowledge Check
Two infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is
 Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πr
Aμ0IπrBμ0Ir(1π+14)CZeroDμ0I2πrTwo infinitely long perpendicular wires carry equal currents in the directions indicated in the following figure. At which of the labeled points is the magnitude of the magnetic field created by the currents the greatest ? Note: All gridlines are equally spaced.
 AABBCCDD
AABBCCDDTwo wires AO and OC carry equal currents i as shown in Fig. One end of both the wires extends to infinity. Angle AOC is α. The magnitude of magnetic field is point P on the bisector of these two wires at a distance r from point O is
 Aμ02πircot(α2)Bμ04πircot(α2)Cμ02πir1+cos(α)2sin(α2)Dμ04πir(α2)
Aμ02πircot(α2)Bμ04πircot(α2)Cμ02πir1+cos(α)2sin(α2)Dμ04πir(α2)
An infinitely long wire carrying current I is bent to from a L shaped wire. Let the bend be the origin and the two arms be along x and y direction (see figure). Calculate the magnitude of magnetic field at point P (in first quadrant) whose co-ordinates are (x, y).

View SolutionA long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
View Solutionone of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
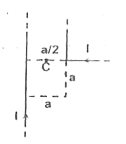
View SolutionA long straight wire, carrying current I, is bent at its midpoint to form an angle of 45∘. Find the induction of magnetic field at point P, distant R from the point of bending (as shown in)

View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
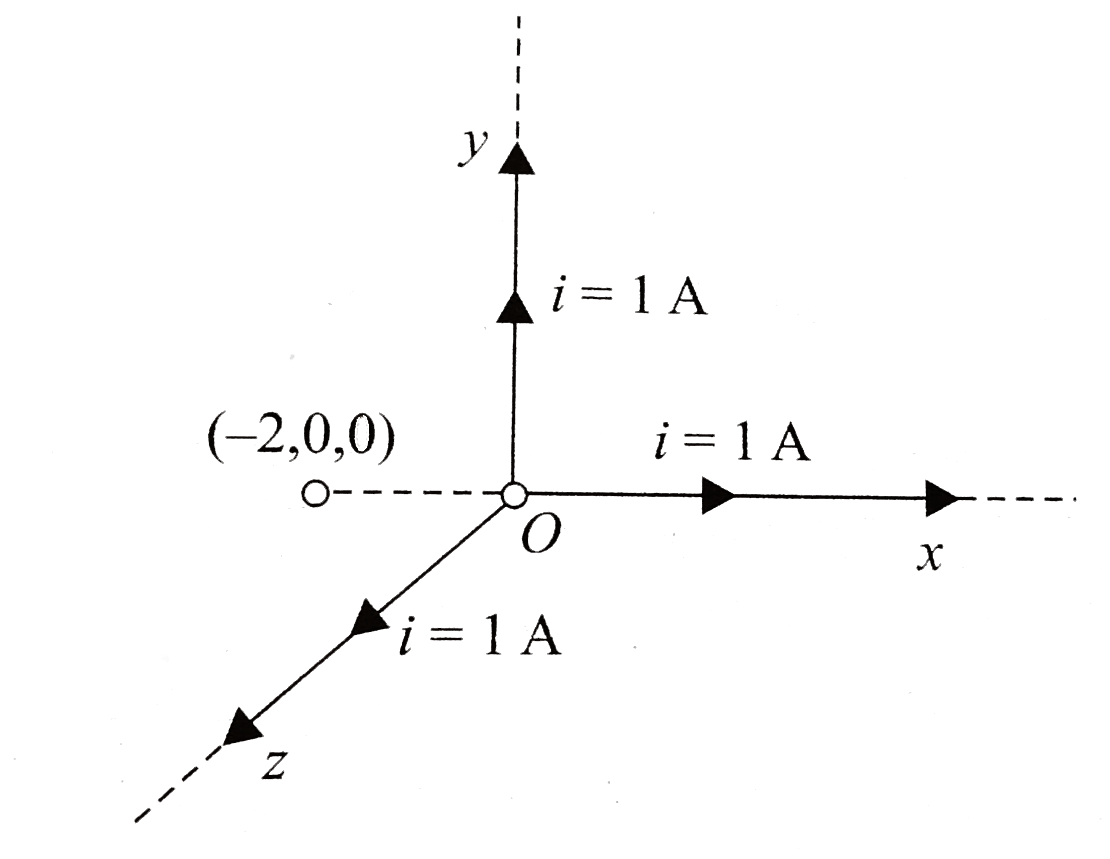
View Solution